Mathematics
Grade9
Easy
Question
The steps of a proof are shown.
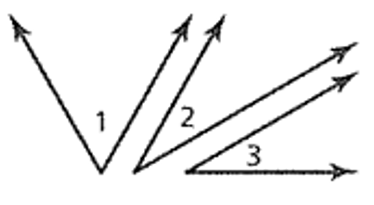
Given 
is a complement of 
.
Prove is a complement of 
What is reason 5?
| Statements | Reasons |
| 1. ∠1 is a complement of ∠2. |
1. Given |
| 2. ∠2 ≡ ∠3 | |
| 3. m ∠ 1 + m ∠ 2 = 90° | |
| 4. m ∠ 2 = m ∠ 3 | |
| 5. m ∠ 1 + m ∠ 3 = 90° | |
| 6. ∠1 is a complement of ∠3. |
- Definition of complementary angles
- Substitution Property of Equality
- Definition of congruent angles
- Subtraction Property of Equality
Hint:
in this question, given is ∠1 is complement of ∠2 and ∠2 ≅∠3, and here prove to ∠1 is a complement of ∠3. We have to give reason of step 5 . for that use the property of equality.
The correct answer is: Substitution Property of Equality
Here , we have to find that reason of step 5.
Firstly , we have is ∠1 is complement of ∠2 and ∠2 ≅∠3
And steps are,
∠1 is complement of ∠2 (given)
∠2 ≅∠3 (given)
m∠1 + m ∠2 = 90 ( complementary angle)
m ∠2 = m ∠3 ( both angle is congruent )
m ∠2 + m ∠3 = 90 ( substitution property )
∠1 is complement of ∠3
Therefore, the reason of step 5 is substitution property of equality.
The correct answer is Substitution property of Equality.
Or,
Substitution Property of Equality
The whole proof:
Statements
Reasons
1. ∠1 is a complement of ∠2.
1. Given
2. ∠2 ≡ ∠3
2. Given
3. m ∠ 1 + m ∠ 2 = 90°
3. Definition of complementary angles
4. m ∠ 2 = m ∠ 3
4. Definition of congruent angles
5. m ∠ 1 + m ∠ 3 = 90°
5. Substitution Property of Equality
6. ∠1 is a complement of ∠3.
6. Definition of complementary angles
In this question, we have to find the reason of step 5 which is substitution property. In substitution property of equality , if X = Y and X = Z then Y = Z.
