Question
The steps of a proof are shown.
Given PQ = RS
Prove PR = QS
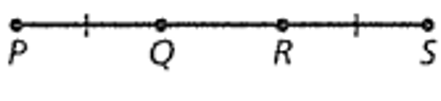
What is the reason for step 5?
| Statements | Reasons |
| 1. PQ = RS | 1. Given |
| 2. PQ + QR = RS + QR | |
| 3. PQ + QR = PR | |
| 4. RS + QR = QS | |
| 5. PR = QS |
- Segment Addition Postulate
- Transitive Property of Equality
- Substitution Property of Equality
- Subtraction Property of Equality

In this question, given is PQ = RS and we have to proved that PR = QS . Here 5 total step were given and also asked the reason of 5th state. This solve by the Segment addition postulate .
The correct answer is: Transitive Property of Equality
Here we have to find the reason of step 5 .
Firstly , we must consider that PQRS as a straight line, and P,Q, R and S are point on it one after another.
Here given is 1 .PQ = RS
2. PQ + QR = RS + QR ( by using addition postulate)
3. PQ + QR = PR ( by segment addition )
4. RS + QR = QS ( by segment addition )
5. PR = QS ( by substitution property both are equal)
Therefore, The reason of step 5 is substitution property of equality.
The correct answer is Substitution property of equality.
Or,
Transitive Property of Equality. The whole proof is as following:
Statements
Reasons
1. PQ = RS
1. Given
2. PQ + QR = RS + QR
2. Addition Property of Equality
3. PQ + QR = PR
3. Segment Addition Postulate (Post. 1.2)
4. RS + QR = QS
4. Segment Addition Postulate (Post. 1.2)
5. PR = QS
5. Transitive Property of Equality
Segment Addition Postulate: The segment addition postulate asserts that if we have two locations on a line segment, A and C, a third point, B, will be found online in segment AC if and only if the distances between the points satisfy the conditions of the equation AB + BC = AC. Transitive Property of Equality: According to the transitive property of equality, all the values of a, b, and c are equal as a = b and b = c, then a = c. In other words, a and c must be equal since items are the same (in this example, b). For instance, x must equal '7' if x = y and y = 7. According to the substitution property of equality, one value can substitute for another in an expression or equation, and the result will still be the same. X and Y can be substituted if their values are the same.
Related Questions to study
The steps of the proof are shown.
GIVEN ⇒ 2AB = AC
PROVE: AB = BC

1. 2AB = AC (Given)
2. AB + AB = AC (____)
3. AB + BC = AC (Segment Addition Postulate)
4. AB + AB = AB + BC (____)
5. AB = BC (Subtraction Property)
What is the reason for step 2?
Distributive Property: A crucial mathematical property that will help you solve many algebraic problems is the distributive property.
The distributive property, also used as the distributive property of multiplication, demonstrates how to solve particular algebraic statements that combine addition and multiplication. For example, a number multiplied by a sum has the same effect as doing each multiplication separately, according to the literal definition of the distributive property.
The distributive property appears in an equation: a(b+c)=ab+ac. The substitution property of equality, if two variables are equal, x and y, respectively, then x can be used in place of y in any equation or expression, and 'y' can is used in place of x.
The steps of the proof are shown.
GIVEN ⇒ 2AB = AC
PROVE: AB = BC

1. 2AB = AC (Given)
2. AB + AB = AC (____)
3. AB + BC = AC (Segment Addition Postulate)
4. AB + AB = AB + BC (____)
5. AB = BC (Subtraction Property)
What is the reason for step 2?
Distributive Property: A crucial mathematical property that will help you solve many algebraic problems is the distributive property.
The distributive property, also used as the distributive property of multiplication, demonstrates how to solve particular algebraic statements that combine addition and multiplication. For example, a number multiplied by a sum has the same effect as doing each multiplication separately, according to the literal definition of the distributive property.
The distributive property appears in an equation: a(b+c)=ab+ac. The substitution property of equality, if two variables are equal, x and y, respectively, then x can be used in place of y in any equation or expression, and 'y' can is used in place of x.
Give the reason for statement #4.
Given: PS = RT, PQ = ST
Prove: QS = RS

| Statement | Reason |
| 1. PS = RT, PQ = ST |
1. |
| 2. PQ + QS = PS |
2. |
| 3. ST + QS = RT |
3. |
| 4. RS + ST = RT |
4. |
| 5. ST + QS = RS + ST |
5. |
| 6. QS = RS |
6. |
Geometrically, a line segment with three collinear points is subject to the segment addition postulate. By the segment addition postulate, point B will only be on the same line segment as points A and C if the sum of AB and BC equals AC if there are two given points on the segment between them, A and C. According to the segment addition postulate, if a line segment has endpoints A and C, and a third point B, then only if the equation AB + BC = AC is true does the third point B lie on the line segment AC. To further comprehend this postulate, look at the illustration provided below.
Give the reason for statement #4.
Given: PS = RT, PQ = ST
Prove: QS = RS

| Statement | Reason |
| 1. PS = RT, PQ = ST |
1. |
| 2. PQ + QS = PS |
2. |
| 3. ST + QS = RT |
3. |
| 4. RS + ST = RT |
4. |
| 5. ST + QS = RS + ST |
5. |
| 6. QS = RS |
6. |
Geometrically, a line segment with three collinear points is subject to the segment addition postulate. By the segment addition postulate, point B will only be on the same line segment as points A and C if the sum of AB and BC equals AC if there are two given points on the segment between them, A and C. According to the segment addition postulate, if a line segment has endpoints A and C, and a third point B, then only if the equation AB + BC = AC is true does the third point B lie on the line segment AC. To further comprehend this postulate, look at the illustration provided below.
Find the measure of each angle in the diagram.

Vertical angles are formed when two lines meet each other at a point. They are always equal to each other. In other words, whenever two lines cross or intersect each other, 4 angles are formed. We can observe that two angles that are opposite to each other are equal and they are called vertical angles.
Find the measure of each angle in the diagram.

Vertical angles are formed when two lines meet each other at a point. They are always equal to each other. In other words, whenever two lines cross or intersect each other, 4 angles are formed. We can observe that two angles that are opposite to each other are equal and they are called vertical angles.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Two angles are said to be supplementary is the sum of their measures is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Two angles are said to be supplementary is the sum of their measures is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Vertical angles are always equal.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Vertical angles are always equal.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

The sum of the angles of a linear pair is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

The sum of the angles of a linear pair is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

The sum of the angles of linear pair is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

The sum of the angles of linear pair is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Vertical angles are always equal.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Vertical angles are always equal.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Here, sum of angles 1 and 2 is 180°.
Two lines that are not perpendicular intersect such that ∠1 and ∠2 are a linear pair, ∠1 and ∠4 are a linear pair, and ∠1 and ∠3 are vertical angles. Tell whether the following statement is true or false.

Here, sum of angles 1 and 2 is 180°.
Which property does the statement illustrate?

Same applies on number and shapes.
Which property does the statement illustrate?

Same applies on number and shapes.
Which property does the statement illustrate?

If a=b, then b = a.
Which property does the statement illustrate?

If a=b, then b = a.
Find the measure of each angle in the diagram.

Find the measure of each angle in the diagram.

Complete the statement with <, >, or =.

If m∠ 4 = 30, then m∠ 5? m∠ 4.
When two angles are formed on a straight line, they are called linear pair.
Complete the statement with <, >, or =.

If m∠ 4 = 30, then m∠ 5? m∠ 4.
When two angles are formed on a straight line, they are called linear pair.
Complete the statement with <, >, or =.

m∠ 8 + m∠ 6? 150
When two angles are formed on a straight line, they are called linear pair.
Complete the statement with <, >, or =.

m∠ 8 + m∠ 6? 150
When two angles are formed on a straight line, they are called linear pair.
What is the reason for statement 2?


| Statement | Reason | |
| 1 | ||
| 2 | ||
| 3 |
Alternate exterior angles are always equal.
What is the reason for statement 2?


| Statement | Reason | |
| 1 | ||
| 2 | ||
| 3 |
Alternate exterior angles are always equal.



