Maths-
General
Easy
Question
If r, s, t are prime numbers and p, q are the positive integers such that the LCM of p, q is  , then the number of ordered pair (p, q) is-
, then the number of ordered pair (p, q) is-
- 224
- 225
- 252S
- 256

At least one of the p and q, must have r,s and t in their prime factorization.
Now, we have to consider each case for selecting the number of ways for power of r, s and t . So, in this way we have to approach the problems.
The correct answer is: 225
Step by step solution :
It is given that 
That is, at least one of p and q must have  ,
,  and
and  in their prime factorizations.
in their prime factorizations.
Now, consider the cases for power of r as follows:
Case 1 : p contains  then q has
then q has  with K = (0,1,2,3)
with K = (0,1,2,3)
That is, number of ways=4.
Case 2 : q contains  then q has
then q has  with K = (0,1,2,3)
with K = (0,1,2,3)
That is, number of ways=4.
Case 3 : Both p and q contains 
Then, number of ways=1.
Therefore, exponent of r may be chosen in 2+2+1=5 ways.
Similarly, exponent of s may be chosen in 4+4+1=9 ways and
Exponent of s may be chosen in 2+2+1=5 ways
Thus, the total number of ways is:

Hence, the number of the ordered pair (p, q) is 225.
Be careful about selecting the r s and t for this particular problem. Because number ways for each selection of r, s and t there are 3 cases. Because there are two values given
p, q . Hence to calculate the total number of ways is to multiply the number of ways for r, number of ways for s and number of ways for t. So, in this way to solve this particular type of problem.
Related Questions to study
Maths-
A rectangle has sides of (2m – 1) & (2n – 1) units as shown in the figure composed of squares having edge length one unit then no. of rectangles which have odd unit length –

A rectangle has sides of (2m – 1) & (2n – 1) units as shown in the figure composed of squares having edge length one unit then no. of rectangles which have odd unit length –

Maths-General
chemistry-
Observe the esterification mechanisms for primary and tertiary alcohols
Type-1: 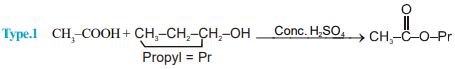

Type-2: 
Mechanism: 
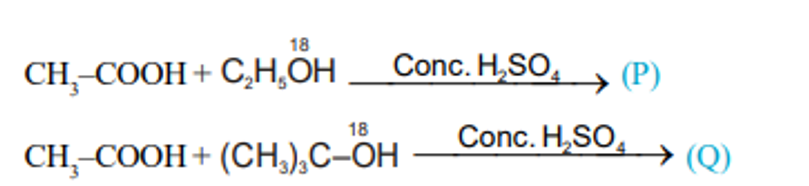
In the above reaction (P) and (Q) are respectively :
Observe the esterification mechanisms for primary and tertiary alcohols
Type-1: 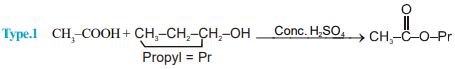

Type-2: 
Mechanism: 

In the above reaction (P) and (Q) are respectively :
chemistry-General
physics-
Two identical samples of a gas are allowed to expand (i) isothermally (ii) adiabatically work done is

Two identical samples of a gas are allowed to expand (i) isothermally (ii) adiabatically work done is

physics-General
physics-
A thermodynamic system is taken from state A to B along ACB and is brought back to Along BDA as Shown in the PV diagram. The net work done during the complete cycle is given by the area.

A thermodynamic system is taken from state A to B along ACB and is brought back to Along BDA as Shown in the PV diagram. The net work done during the complete cycle is given by the area.

physics-General
physics-
An ideal gas is taken V path ACBA as Shown in figure, The net work done in the whole cycle is

An ideal gas is taken V path ACBA as Shown in figure, The net work done in the whole cycle is

physics-General
physics-
In the Cyclic Process shown is the figure, the work done by the gas in one cycle

In the Cyclic Process shown is the figure, the work done by the gas in one cycle

physics-General
physics-
A Cyclic process is Shown in the PT diagram. Which of the curve show the same process on a VT diagram?

A Cyclic process is Shown in the PT diagram. Which of the curve show the same process on a VT diagram?

physics-General
physics-
The M.I of a disc of mass M and radius R about an axis passing through the centre O and perpendicular to the plane of dise is If one quarter of the disc is removed the new moment of inertia of disc will be....

The M.I of a disc of mass M and radius R about an axis passing through the centre O and perpendicular to the plane of dise is If one quarter of the disc is removed the new moment of inertia of disc will be....

physics-General
physics-
Work done in the given P V diagram in the cyclic process is
V diagram in the cyclic process is

Work done in the given P V diagram in the cyclic process is
V diagram in the cyclic process is

physics-General
physics-
In the following indicators diagram, the net amount of work done will be

In the following indicators diagram, the net amount of work done will be

physics-General
physics-
In P V diagramgiven below, the isochoric, isothermal and isobaric path respectively are
V diagramgiven below, the isochoric, isothermal and isobaric path respectively are

In P V diagramgiven below, the isochoric, isothermal and isobaric path respectively are
V diagramgiven below, the isochoric, isothermal and isobaric path respectively are

physics-General
Maths-
The number of ways to fill each of the four cells of the table with a distinct natural number such that the sum of the numbers is 10 and the sums of the numbers placed diagonally are equal, is-

The number of ways to fill each of the four cells of the table with a distinct natural number such that the sum of the numbers is 10 and the sums of the numbers placed diagonally are equal, is-

Maths-General
physics-
ideal gas at 27°C is Compressed adiabatically, to  of its original Volume. If
of its original Volume. If  , then the rise in temperature is
, then the rise in temperature is
ideal gas at 27°C is Compressed adiabatically, to  of its original Volume. If
of its original Volume. If  , then the rise in temperature is
, then the rise in temperature is
physics-General
physics-
An ideal gas is taken through the cycle A B
B C
C A as shown in the figure, If the net heat supplied to the gas in the cycle is
A as shown in the figure, If the net heat supplied to the gas in the cycle is  , the work done by the gas in the process C
, the work done by the gas in the process C A is
A is

An ideal gas is taken through the cycle A B
B C
C A as shown in the figure, If the net heat supplied to the gas in the cycle is
A as shown in the figure, If the net heat supplied to the gas in the cycle is  , the work done by the gas in the process C
, the work done by the gas in the process C A is
A is

physics-General
physics-
Acyclic Process ABCD is Shown in the P V diagam. which of the following curves represent the same Represent the same Process?
V diagam. which of the following curves represent the same Represent the same Process?

Acyclic Process ABCD is Shown in the P V diagam. which of the following curves represent the same Represent the same Process?
V diagam. which of the following curves represent the same Represent the same Process?

physics-General



