Maths-
General
Easy
Question
If 
then 
- 1
- 2
- 3
- 4
Hint:
We are given a function u. It is a function of three variables. We have to find the value of 
. We will take the partial derivative of the function w.r.t to the variables and multiply with the respective variables. Then we will add them up.
The correct answer is: 3
The given function is u=log(x3+y3+z3-3xyz)
We have to find the value of
It means we have to find the value of 
For simplification we will write u=logv
v = x3 + y3 + z3 -3xyz
We will take the partial derivative of u w.r.t all three variables.
Now, we will substitute all the values in the .
The required answer is 3.
The variable v is used just for simplification. When we take partial derivative w.r.t to certain variable, we keep other variables constant.
Related Questions to study
chemistry-
Which type of isomerism is observed between I and II
and 
Which type of isomerism is observed between I and II
and
chemistry-General
chemistry-
How many spatial orientations are possible in following compounds-
How many spatial orientations are possible in following compounds-
chemistry-General
chemistry-
The configuration of stereo center in the compound is –
The configuration of stereo center in the compound is –
chemistry-General
chemistry-
The IUPAC name of the given compound –
The IUPAC name of the given compound –
chemistry-General
chemistry-
Shows which type of isomerism
and 
Shows which type of isomerism
and
chemistry-General
chemistry-
The two compounds shown below are –
The two compounds shown below are –
chemistry-General
chemistry-
The compound whose stereo- chemical formula is written below exhibits ‘x’ geometrical isomers and ‘y’ optical isomers :
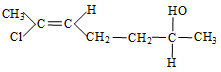
The value of x and y are :
The compound whose stereo- chemical formula is written below exhibits ‘x’ geometrical isomers and ‘y’ optical isomers :
The value of x and y are :
chemistry-General
chemistry-
The correct statements about the compounds a, b and c is/are
The correct statements about the compounds a, b and c is/are
chemistry-General
chemistry-
The absolute configuration of the following compound is :
The absolute configuration of the following compound is :
chemistry-General
chemistry-
The name of the compound is
The name of the compound is
chemistry-General
chemistry-
The correct statement(s) about the compound given below is (are)
The correct statement(s) about the compound given below is (are)
chemistry-General
chemistry-
If 
in above compound is rotated by 
angle in anticlockwise direction along 
, which of the following form will be produced :
If in above compound is rotated by angle in anticlockwise direction along , which of the following form will be produced :
chemistry-General
chemistry-
The absolute configuration of
The absolute configuration of
chemistry-General
chemistry-
The correct IUPAC name of the compound is
The correct IUPAC name of the compound is
chemistry-General
chemistry-
The interchange of two groups (Br and 
) at the chiral centre of the projection formula (I) yields the formula (II), while the interchange of another set of two groups (
and Cl) of (I) yields the projection formula (III).
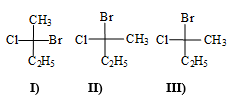
Which of the following statements is not correct about the structures (I), (II) and (III) -
The interchange of two groups (Br and ) at the chiral centre of the projection formula (I) yields the formula (II), while the interchange of another set of two groups ( and Cl) of (I) yields the projection formula (III).
Which of the following statements is not correct about the structures (I), (II) and (III) -
chemistry-General
