Maths-
General
Easy
Question
If 
for 
, then 
- 0
- 1
- 2
- 3
The correct answer is: 1
Related Questions to study
maths-
The largest value of r satisfying inequality 20Cr 
20Cr – 1 is -
The largest value of r satisfying inequality 20Cr 20Cr – 1 is -
maths-General
maths-
A double decker bus can accommodate (u + 
) passengers, u in the upper deck and in the lower deck. The number of ways in which the (u + ) passengers can be distributed in the two decks, if r (
) particular passengers refuse to go in the upper deck and S(
u) refuse to sit in the lower deck, is -
A double decker bus can accommodate (u + ) passengers, u in the upper deck and in the lower deck. The number of ways in which the (u + ) passengers can be distributed in the two decks, if r () particular passengers refuse to go in the upper deck and S(u) refuse to sit in the lower deck, is -
maths-General
maths-
Domain of f(x) = log10(log10(1 + x3)) is -
Domain of f(x) = log10(log10(1 + x3)) is -
maths-General
chemistry-
The correct orders about compounds I and II are:
i) 
ii) 
The correct orders about compounds I and II are:
i)
ii)
chemistry-General
chemistry-
Which of the following is correct method for separating a mixture of following compounds?
Which of the following is correct method for separating a mixture of following compounds?
chemistry-General
chemistry-
The order in which the reagent must be used to separate the compound I - IV is:
The order in which the reagent must be used to separate the compound I - IV is:
chemistry-General
chemistry-
Decreasing order of solubility of following compounds is:
i) 
ii) 
iii) 
iv) 
Decreasing order of solubility of following compounds is:
i)
ii)
iii)
iv)
chemistry-General
chemistry-
Which of the following statement is correct about tropolone?
Which of the following statement is correct about tropolone?
chemistry-General
chemistry-
In which case first has higher solubility than second?
I) Phenol, Benzene
II) Nitrobenzene, Phenol
III) o–Hydroxybenzaldehyde, p–Hydroxy benzaldehyde
IV) CH3CHO, CH3–O–CH3
V) o–Nitrophenol, p–Nitrophenol
VI) 
In which case first has higher solubility than second?
I) Phenol, Benzene
II) Nitrobenzene, Phenol
III) o–Hydroxybenzaldehyde, p–Hydroxy benzaldehyde
IV) CH3CHO, CH3–O–CH3
V) o–Nitrophenol, p–Nitrophenol
VI)
chemistry-General
chemistry-
Arrange the following in decreasing order of their solubility in water
Arrange the following in decreasing order of their solubility in water
chemistry-General
maths-
18 points are indicated on the perimeter of a triangle ABC (see figure). How many triangle are there with vertices at these points ?
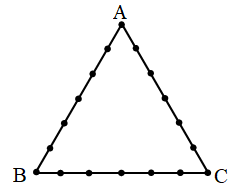
18 points are indicated on the perimeter of a triangle ABC (see figure). How many triangle are there with vertices at these points ?
maths-General
Maths-
If A and B are two events such that 
and 
then A and B are
If A and B are two events such that and then A and B are
Maths-General
maths-
Number of rectangles in the grid shown which are not squares is:
Number of rectangles in the grid shown which are not squares is:
maths-General
maths-
If 
and 
then 
If and then
maths-General
chemistry-
The correct order of solubility in water is:
a) CH3OH
b) CH3CH2OH
c) 
d) 
The correct order of solubility in water is:
a) CH3OH
b) CH3CH2OH
c)
d)
chemistry-General
