Question
If the angles of triangle are in the ratio 1:1:4 then ratio of the perimeter of triangle to its largest side



- 3:2

The law of sines says that the ratio of the sine of one angle to the opposite side is the same ratio for all three angles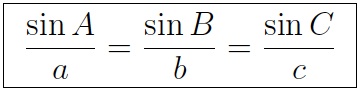 .
.
The correct answer is: 

If the angles of triangle are in the ratio 1:1:4 .

If a triangle has sides a, b, and c, then the perimeter of that triangle will be P = a + b + c
According to question,
Ratio of the perimeter of triangle to its largest side.. 
If a triangle has sides a, b, and c, then the perimeter of that triangle will be P = a + b + c
According to question,
Ratio of the perimeter of triangle to its largest side..
if a triangle has sides a, b, and c, then the perimeter of that triangle will be P = a + b + c .
Related Questions to study
The pressure on a swimmer 20 m below the surface of coater at sea level is
The pressure on a swimmer 20 m below the surface of coater at sea level is
 can’t be stored in
can’t be stored in
 can’t be stored in
can’t be stored in
The angles of a triangle are in the ratio 3:5:10. Then ratio of smallest to greatest side is
A triangle has sides a, b, and c, then the perimeter of that triangle will be P = a + b + c.
The angles of a triangle are in the ratio 3:5:10. Then ratio of smallest to greatest side is
A triangle has sides a, b, and c, then the perimeter of that triangle will be P = a + b + c.
Consider a body as shown in figure, consisting of two identical bulls, each of mass M connected by a light rigid rod. If an impulse J=MV is imparted to the body at one of its ends, what would be its angular velocity. What is V ?

Consider a body as shown in figure, consisting of two identical bulls, each of mass M connected by a light rigid rod. If an impulse J=MV is imparted to the body at one of its ends, what would be its angular velocity. What is V ?

11H2 1H and 3 1H will have the same
11H2 1H and 3 1H will have the same
The sides of a triangle are  and
and  for some
for some  .Then the greatest angle of the triangle is
.Then the greatest angle of the triangle is
The law of cosines generalizes the Pythagorean formula to all triangles. It says that c2, the square of one side of the triangle, is equal to a2 + b2, the sum of the squares of the the other two sides, minus 2ab cos C, twice their product times the cosine of the opposite angle. When the angle C is right, it becomes the Pythagorean formula.
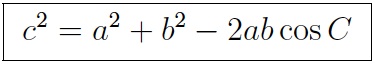
The sides of a triangle are  and
and  for some
for some  .Then the greatest angle of the triangle is
.Then the greatest angle of the triangle is
The law of cosines generalizes the Pythagorean formula to all triangles. It says that c2, the square of one side of the triangle, is equal to a2 + b2, the sum of the squares of the the other two sides, minus 2ab cos C, twice their product times the cosine of the opposite angle. When the angle C is right, it becomes the Pythagorean formula.
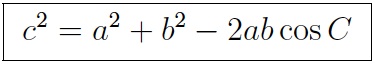
A cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in figure. It hits a ridge at point O. The angular speed of the block after it hits 0 is
A cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in figure. It hits a ridge at point O. The angular speed of the block after it hits 0 is
A uniform rod of length 2 L is placed with one end in contact with horizontal and is then inclined at an angle  to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be.....
to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be.....
A uniform rod of length 2 L is placed with one end in contact with horizontal and is then inclined at an angle  to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be.....
to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be.....
If the sides of a triangle are in the ratio then greatest angle is
If the sides of a triangle are in the ratio then greatest angle is
A straight rod of length L has one of its ends at the origin and the other end at x=L If the mass per unit length of rod is given by Ax where A is constant where is its center of mass.
A straight rod of length L has one of its ends at the origin and the other end at x=L If the mass per unit length of rod is given by Ax where A is constant where is its center of mass.
In  then
then 
s denotes the semi-perimeter of the triangle ABC, ∆ its area and R the radius of the circle circumscribing the triangle ABC i.e., R is the circum-radius.
In  then
then 
s denotes the semi-perimeter of the triangle ABC, ∆ its area and R the radius of the circle circumscribing the triangle ABC i.e., R is the circum-radius.



