Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

Integrating factor of the differential equation $cos space x fraction numerator d y over denominator d x end fraction plus y sin space x equals 1$ is

$\cos x$
tan x
sec x
sin x

hint Hint:

In the question we have to find the integrating factor of the equation. For this we will first arrange the equation in the form of $fraction numerator d y over denominator d x end fraction plus a y equals b$ and IF = $e to the power of integral a space d x end exponent$ .

The correct answer is: sec x

$G i v e n comma space cos space x fraction numerator d y over denominator d x end fraction plus y sin space x equals 1 rightwards double arrow fraction numerator d y over denominator d x end fraction plus fraction numerator sin x over denominator cos x end fraction y equals fraction numerator 1 over denominator cos x end fraction rightwards double arrow fraction numerator d y over denominator d x end fraction plus tan x space. y equals s e c x I. F equals e to the power of integral tan x space d x end exponent equals e to the power of log space s e c x end exponent equals s e c x$

Related Questions to study

The equivalent capacitance of the combination of the capacitors is

The equivalent capacitance of the combination of the capacitors is

physics-General

Four plates of equal area $A$ are separated by equal distance $d$ and are arranged as shown in the figure. The equivalent capacity is

Four plates of equal area $A$ are separated by equal distance $d$ and are arranged as shown in the figure. The equivalent capacity is

physics-General

Solution of differential equation $fraction numerator d y over denominator d x end fraction plus a y equals e to the power of m x end exponent$ is

Solution of differential equation $fraction numerator d y over denominator d x end fraction plus a y equals e to the power of m x end exponent$ is

parallel

In given circuit when switch $S$ has been closed then charge on capacitor $A$ and $B$ respectively are

In given circuit when switch $S$ has been closed then charge on capacitor $A$ and $B$ respectively are

physics-General

Solution of differential equation $d y minus sin space x sin y space d x equals 0$ is

Solution of differential equation $d y minus sin space x sin y space d x equals 0$ is

In the given figure, a hollow spherical capacitor is shown. The electric field will not be zero at

In the given figure, a hollow spherical capacitor is shown. The electric field will not be zero at

physics-General

parallel

In the capacitor shown in the circuit is changed to 5 V and left in the circuit, in 12s the charge on the capacitor will become $left parenthesis e equals 2.718 right parenthesis$

In the capacitor shown in the circuit is changed to 5 V and left in the circuit, in 12s the charge on the capacitor will become $left parenthesis e equals 2.718 right parenthesis$

physics-General

The solution of the differential equation $2 x fraction numerator d y over denominator d x end fraction minus y equals 3$ represent

The solution of the differential equation $2 x fraction numerator d y over denominator d x end fraction minus y equals 3$ represent

The stress - strain graphs for materials A and B are as shown. Choose the correct alternative

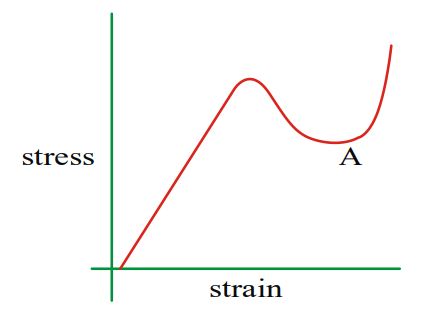
The stress - strain graphs for materials A and B are as shown. Choose the correct alternative

physics-General

parallel

In the experiment to determine Young’s modulus of the material of a wire under tension used in the arrangement as shown. The percentage error in the measurement of length is ‘a’, in the measurement of the radius of the wire is ‘b’ and in the measurement of the change in length of the wire is ‘c’. Percentage error in the measurement of Young’s modulus for a given load is

In the experiment to determine Young’s modulus of the material of a wire under tension used in the arrangement as shown. The percentage error in the measurement of length is ‘a’, in the measurement of the radius of the wire is ‘b’ and in the measurement of the change in length of the wire is ‘c’. Percentage error in the measurement of Young’s modulus for a given load is

physics-General

The graph shows the change ' ' Dl in the length of a thin uniform wire used by the application of force ‘F’ at different temperatures T₁ and T₂ The variation suggests that

The graph shows the change ' ' Dl in the length of a thin uniform wire used by the application of force ‘F’ at different temperatures T₁ and T₂ The variation suggests that

physics-General

The load versus extension graph for four wires of same material is shown. The thinnest wire is represented by the line

The load versus extension graph for four wires of same material is shown. The thinnest wire is represented by the line

physics-General

parallel

A 2 $mu F$ capacitor is charged as shown in the figure. The percentage of its stored energy dissipated after the switch $s$ is turned to positions 2 is

A 2 $mu F$ capacitor is charged as shown in the figure. The percentage of its stored energy dissipated after the switch $s$ is turned to positions 2 is

physics-General

What is the potential difference between points $A a n d B$ in the circuit shown?

What is the potential difference between points $A a n d B$ in the circuit shown?

physics-General

If m and n are order and degree of the equation $open parentheses fraction numerator d squared y over denominator d x squared end fraction close parentheses to the power of 5 plus 4 times fraction numerator open parentheses fraction numerator d squared y over denominator d x squared end fraction close parentheses cubed over denominator fraction numerator d cubed y over denominator d x cubed end fraction end fraction plus fraction numerator d cubed y over denominator d x cubed end fraction equals x squared minus 1$ then

If m and n are order and degree of the equation $open parentheses fraction numerator d squared y over denominator d x squared end fraction close parentheses to the power of 5 plus 4 times fraction numerator open parentheses fraction numerator d squared y over denominator d x squared end fraction close parentheses cubed over denominator fraction numerator d cubed y over denominator d x cubed end fraction end fraction plus fraction numerator d cubed y over denominator d x cubed end fraction equals x squared minus 1$ then

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.