The number of ways to fill each of the four cells of the table with a distinct natural number such that the sum of the numbers is 10 and the sums of the numbers placed diagonally are equal, is-

The correct answer is: 8

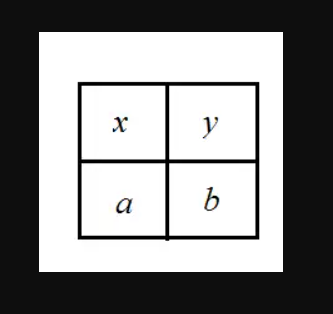
According to question $x+b=a+y$and $x+y+a+b=10$
$\mathrm{So x + b= 5 and a + y= 5}$
$\mathrm{Given:\; all\; number\; should\; be\; different\; and two\; pairs\; whose\; sum\; is 5.}$
$\mathrm{We\; have 2 pair\; of\; natural\; number\; that\; is (1,4),(2,3) whose\; sum\; is 5}$
$\mathrm{We\; can\; choose 1 pair\; among 2 of\; them\; for (x, b) by 2! ways\; and\; they\; can\; rearranged\; in 2! ways.}$
$\mathrm{So\; total\; ways\; for (x, b) will\; be 2!\times 2!}$
$\mathrm{Remaining\; one\; pair\; will\; be\; for (a, y) and\; they\; can\; be\; arranged\; by 2! ways.}$
$\mathrm{So\; total\; ways\; for (y, a) will\; be 2!.}$
$\mathrm{Combining\; both\; situation\; together\; we\; get 2! \times 2! \times 2!= 8}$