Physics-
General
Easy
Question
Consider a disc rotating in the horizontal plane with a constant angular speed 
about its centre 
. The disc has a shaded region on one side of the diameter and an unshanded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles 
and 
are simultaneously projected at an angle towards 
. The velocity of projection is in the 
plane and is same for both pebbles with respect to the disc. Assume that i) they land back on the disc before the disc has completed 
rotation. ii) their range is less than half the disc radius, and iii) remains constant throughout. Then
- lands in the shaded region and in the unshaded region
- lands in the unshaded region and in the shaded region
- Both and land in the unshaded region
- Both and land in the shaded region
lands in the shaded region and in the unshaded region
lands in the unshaded region and in the shaded region
and land in the unshaded region
and land in the shaded region
The correct answer is: lands in the shaded region and in the unshaded region
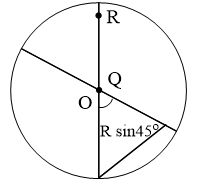
To reach the unshaded portion particle needs to travel horizontal range greater than 
or 
but its range is less than 
. So it will fall on shaded portion
is near to origin, its velocity will be nearly along 
so its will fall in unshaded portion
Related Questions to study
physics-
The resultant of a system of forces shown in figure is a force of 10 N parallel to given forces through , where 
equals
The resultant of a system of forces shown in figure is a force of 10 N parallel to given forces through , where equals
physics-General
chemistry-
On reacting with neutral ferric chloride, phenol gives
On reacting with neutral ferric chloride, phenol gives
chemistry-General
physics-
An air bubble in glass (m =1.5) is situated at a distance 3 cm from a convex surface of diameter 10 cm as shown The distance from surface at which the image of bubble appears is
An air bubble in glass (m =1.5) is situated at a distance 3 cm from a convex surface of diameter 10 cm as shown The distance from surface at which the image of bubble appears is
physics-General
physics-
The fig shows a mixture of blue, green, red colours incident on a right angled prism The critical angles of the material of prism for red, green and blue colours are 460 , 440 , 430 respectively, The arrangement will separate
The fig shows a mixture of blue, green, red colours incident on a right angled prism The critical angles of the material of prism for red, green and blue colours are 460 , 440 , 430 respectively, The arrangement will separate
physics-General
chemistry-
Ethanol reacts with thionyl chloride to give ethyl chloride and:
Ethanol reacts with thionyl chloride to give ethyl chloride and:
chemistry-General
physics-
The minimum speed for a particle at the lowest point of a vertical circle of radius 
, to describe the circle is 
. If the radius of the circle is reduced to one-fourth its value, the corresponding minimum speed will be
The minimum speed for a particle at the lowest point of a vertical circle of radius , to describe the circle is . If the radius of the circle is reduced to one-fourth its value, the corresponding minimum speed will be
physics-General
chemistry-
Scientific aspect of fermentation was first studied by:
Scientific aspect of fermentation was first studied by:
chemistry-General
physics-
The convex surface of a thin concav–convex lens of glass of refractive index 1.5 has a radius of curvature of 20 cm The concave surface has a radius of curvature of 60 cm The convex side is silvered and placed on a horizontal surface as shown in the figure A small object is placed on the principal axis of the combination, at a distance of 30 cm in front of the mirror The magnification of the image is
The convex surface of a thin concav–convex lens of glass of refractive index 1.5 has a radius of curvature of 20 cm The concave surface has a radius of curvature of 60 cm The convex side is silvered and placed on a horizontal surface as shown in the figure A small object is placed on the principal axis of the combination, at a distance of 30 cm in front of the mirror The magnification of the image is
physics-General
physics-
The convex surface of a thin concav–convex lens of glass of refractive index 1.5 has a radius of curvature of 20 cm The concave surface has a radius of curvature of 60 cm The convex side is silvered and placed on a horizontal surface as shown in the figure The combination behaves like
The convex surface of a thin concav–convex lens of glass of refractive index 1.5 has a radius of curvature of 20 cm The concave surface has a radius of curvature of 60 cm The convex side is silvered and placed on a horizontal surface as shown in the figure The combination behaves like
physics-General
physics-
The convex surface of a thin concav–convex lens of glass of refractive index 1.5 has a radius of curvature of 20 cm The concave surface has a radius of curvature of 60 cm The convex side is silvered and placed on a horizontal surface as shown in the figure The focal length of the combination has the magnitude
The convex surface of a thin concav–convex lens of glass of refractive index 1.5 has a radius of curvature of 20 cm The concave surface has a radius of curvature of 60 cm The convex side is silvered and placed on a horizontal surface as shown in the figure The focal length of the combination has the magnitude
physics-General
physics-
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2m It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure
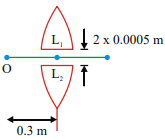
Separation between the images is
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2m It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure
Separation between the images is
physics-General
physics-
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2m It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure
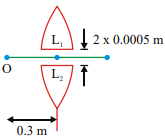
Number of images found is
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2m It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure
Number of images found is
physics-General
physics-
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2m It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure
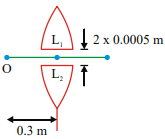
Image will be formed from the lens at a distance of
A point object O is placed at a distance of 0.3 m from a convex lens of focal length 0.2m It is then cut into two halves each of which is displaced by 0.0005 m as shown in figure
Image will be formed from the lens at a distance of
physics-General
chemistry-
The major product obtained on interaction of phenol with sodium hydroxide and carbon dioxide is
The major product obtained on interaction of phenol with sodium hydroxide and carbon dioxide is
chemistry-General
chemistry-
Which will not form a yellow precipitate on heating with an alkaline solution of iodine?
Which will not form a yellow precipitate on heating with an alkaline solution of iodine?
chemistry-General
