Physics-
General
Easy
Question
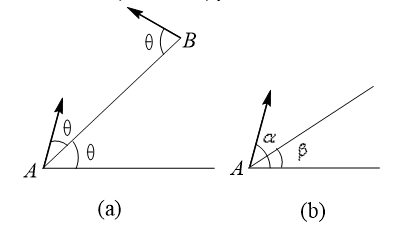
From an inclined plane two particles are projected with same speed at same angle 
, one up and other down the plane as shown in figure. Which of the following statements 
is/are correct?
- The time of flight of each particle is the same.
- The particles will collide the plane with same speed
- Both the particles strike the plane perpendicularly
- The particles will collide in mid air if projected simultaneously and time of flight of each particle is less than the time of collision
The correct answer is: The time of flight of each particle is the same.
Here, 
Time of flight of 
is, 
Time of flight of 
is, 
So, 
. The acceleration of both the particles is 
downwards. Therefore, relative acceleration between the two is zero or relative motion between the two is uniform. The relative velocity of w.r.t. is towards 
, therefore collision will take place between the two in mid air.
Related Questions to study
Physics-
Two particles 1 and 2 are projected with same speed 
as shown in figure. Particle 2 is on the ground and particle 1 is at a height 
from the ground and at a horizontal distance 
from particle 2. If a graph is plotted between and for the condition of collision of the two then ( on 
-axis and on 
-axis
Two particles 1 and 2 are projected with same speed as shown in figure. Particle 2 is on the ground and particle 1 is at a height from the ground and at a horizontal distance from particle 2. If a graph is plotted between and for the condition of collision of the two then ( on -axis and on -axis
Physics-General
physics-
a) Name the experiment for which the adjacent graph, showing the variation of intensity of scattered electrons with the angle of scatter ing (q) was obtained.
b) Also name the important hypothesis that was confirmed by this experiment
a) Name the experiment for which the adjacent graph, showing the variation of intensity of scattered electrons with the angle of scatter ing (q) was obtained.
b) Also name the important hypothesis that was confirmed by this experiment
physics-General
physics-
Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is 
, then the ratio of tensions in the three sections of the string is
Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is , then the ratio of tensions in the three sections of the string is
physics-General
physics-
A ball of mass
kg is attached to the end of a string having length 
0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is
A ball of mass kg is attached to the end of a string having length 0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is
physics-General
maths-
The ellipse 
and the straight line y = mx + c intersect in real points only if
The ellipse and the straight line y = mx + c intersect in real points only if
maths-General
Physics-
A boy throws a cricket ball from the boundary to the wicket-keeper. If the frictional force due to air cannot be ignored, the forces acting on the ball at the position X are respected by
A boy throws a cricket ball from the boundary to the wicket-keeper. If the frictional force due to air cannot be ignored, the forces acting on the ball at the position X are respected by
Physics-General
physics-
Four capacitors are connected as shown in figure. The equivalent capacitance between and is
Four capacitors are connected as shown in figure. The equivalent capacitance between and is
physics-General
physics-
A frictionless track 
ends in a circular loop of radius 
figure. A body slides down the track from point which is at a height 
cm. Maximum value of 
for the body to successfully complete the loop is
A frictionless track ends in a circular loop of radius figure. A body slides down the track from point which is at a height cm. Maximum value of for the body to successfully complete the loop is
physics-General
physics-
In a circuit shown in figure, the potential difference across the capacitor of 2 F is
In a circuit shown in figure, the potential difference across the capacitor of 2 F is
physics-General
physics-
The effective capacitance between points 
and 
shown in figure. Assuming 
F and that outer capacitors are all 
F is
The effective capacitance between points and shown in figure. Assuming F and that outer capacitors are all F is
physics-General
physics-
The four capacitors, each of 25 
F are connected as shown in figure. The DC voltmeter reads 200 V. the change on each plate of capacitor is
The four capacitors, each of 25 F are connected as shown in figure. The DC voltmeter reads 200 V. the change on each plate of capacitor is
physics-General
physics-
For the circuit shown in figure the charge on 4F capacitor is
For the circuit shown in figure the charge on 4F capacitor is
physics-General
Physics-
A particle originally at a rest at the highest point of a smooth circle in a vertical plane, is gently pushed and starts sliding along the circle. It will leave the circle at a vertical distance below the highest point such that
A particle originally at a rest at the highest point of a smooth circle in a vertical plane, is gently pushed and starts sliding along the circle. It will leave the circle at a vertical distance below the highest point such that
Physics-General
Maths-
Polar of origin (0, 0) w.r.t. the circle 
touches the circle 
, if
Polar of origin (0, 0) w.r.t. the circle touches the circle , if
Maths-General
physics-
Electrons ejected from the surface of a metal, when light of certain frequency is incident on it, are stopped fully by a retarding potential of 3 volts Photo electric effect in this metallic surface begins at a frequency 6 x 1014s -1 The frequency of the incident light in s-1 is [h=6 x 10-34J-sec;charge on the electron=1.6x10-19C]
Electrons ejected from the surface of a metal, when light of certain frequency is incident on it, are stopped fully by a retarding potential of 3 volts Photo electric effect in this metallic surface begins at a frequency 6 x 1014s -1 The frequency of the incident light in s-1 is [h=6 x 10-34J-sec;charge on the electron=1.6x10-19C]
physics-General
