Question
Three charges  and
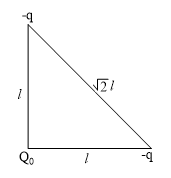
and  are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if
are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if  is equal to
is equal to




- +q
The correct answer is: 
Here total electrostatic potential energy is zero

On solving,

Related Questions to study
A hollow conducting sphere is placed in an electric field produced by a point charge placed at P as shown in figure.  be the potentials at points A, B and C respectively. Then
be the potentials at points A, B and C respectively. Then

A hollow conducting sphere is placed in an electric field produced by a point charge placed at P as shown in figure.  be the potentials at points A, B and C respectively. Then
be the potentials at points A, B and C respectively. Then

The figure shows electric potential V as a function of  . Rank the four regions according to the magnitude of
. Rank the four regions according to the magnitude of  -component of the electric field E within them, greatest first
-component of the electric field E within them, greatest first

The figure shows electric potential V as a function of  . Rank the four regions according to the magnitude of
. Rank the four regions according to the magnitude of  -component of the electric field E within them, greatest first
-component of the electric field E within them, greatest first

The general solution of the equation  is
is
The general solution of the equation  is
is
Solution of  is given by
is given by
Solution of  is given by
is given by
Equation of the curve passing through (3, 9) which satisfies the differential equation  is
is
Equation of the curve passing through (3, 9) which satisfies the differential equation  is
is
If  and f(1) = 2, then f(3) =
and f(1) = 2, then f(3) =
If  and f(1) = 2, then f(3) =
and f(1) = 2, then f(3) =
The degree and order of the differential equation of all tangent lines to the parabola x2 = 4y is:
The degree and order of the differential equation of all tangent lines to the parabola x2 = 4y is:
The differential equation of all non-horizontal lines in a plane is :
The differential equation of all non-horizontal lines in a plane is :
The differential equation of all non-vertical lines in a plane is :
The differential equation of all non-vertical lines in a plane is :
The differential equation of all conics with the coordinate axes, is of order
The differential equation of all conics with the coordinate axes, is of order
If the algebraic sum of distances of points (2, 1) (3, 2) and (-4, 7) from the line y = mx + c is zero, then this line will always pass through a fixed point whose coordinate is
If the algebraic sum of distances of points (2, 1) (3, 2) and (-4, 7) from the line y = mx + c is zero, then this line will always pass through a fixed point whose coordinate is



