Maths-
General
Easy
Question
Ramesh and Mahesh solve an equation. In solving Ramesh commits a mistake in constant term and finds the roots 8 and 2. Mahesh commits a mistake in the coefficient of x and finds the roots – 9 and – 1. The correct roots are
- – 8, 2
- 9, 1
- 9, - 1
- – 8, - 2

The definition of a quadratic as a second-degree polynomial equation demands that at least one squared term must be included. With the use of the factorization approach, we will create two quadratic equations from two sets of roots found by Ramesh and Mahesh for a general quadratic equation.
The correct answer is: 9, 1
The quadratic equation has the following generic form ax² + bx + c = 0 where a, b, and c are numerical coefficients and x is an unknown variable. Here, an is greater than zero because if it equals zero, the equation will cease to be quadratic and change to a linear equation, such as bx+c=0.
A number is swiftly factorised into smaller numbers or factors of the number using the factorization formula. A factor is a number that evenly divides the inputted number. There are a maximum of n real roots that can exist for a polynomial of degree n.
Mahesh makes a mistake in the coefficient of x, and we learn that the roots of the equation are -9 and -1.
We will use factorization method to form a quadratic equation as we have roots of quadratic equation that are -9 and -1.
Then the quadratic equation will be:
(x−(−9))(x−(−1))=0
(x+9)(x+1)=0
⇒x2+10x+9=0
Now comparing it with ax² + bx + c = 0, we get:
a=1,b=10,c=9
Now we have given that Mahesh commits a mistake in calculating the coefficient of x i.e. ‘b’ so b≠10 then a=1,c=9, then we get:
a=1,b=−10,c=9
Substitute the values of a, b and c in ax² + bx + c = 0, we get:
⇒ −10x+9=0
−10x+9=0
 −10x+9=0
Use the factorization method to find the roots of equation (4)
−10x+9=0
Use the factorization method to find the roots of equation (4)
We can write equation (4) as
⇒ −x−9x+9=0
−x−9x+9=0 Factorising it, we get:
Factorising it, we get:
( x − 1 ) ( x − 9 ) = 0 x = 1 and x = 9.
(x+9)(x+1)=0
Here we were given that in solving Ramesh commits a mistake in constant term and finds the roots 8 and 2. Many might create incorrect quadratic equations using the provided roots because they don't multiply carefully, which results in errors in one of the equation's signs. So the solution is 9, 1.
Related Questions to study
physics-
Three particles, each of mass m, are placed at the corners of right angled triangle as shown in Fig. If OA=a and OB=b, the position vector of the centre of mass is (here i and j are unit vectors along  and
and  axes respectively).
axes respectively).

Three particles, each of mass m, are placed at the corners of right angled triangle as shown in Fig. If OA=a and OB=b, the position vector of the centre of mass is (here i and j are unit vectors along  and
and  axes respectively).
axes respectively).

physics-General
physics-
Four point masses  and
and  are placed on a plane as shown in figure. If the co-ordinates of the centre of mass of the system be
are placed on a plane as shown in figure. If the co-ordinates of the centre of mass of the system be  then the values of
then the values of  and
and  are respectively
are respectively

Four point masses  and
and  are placed on a plane as shown in figure. If the co-ordinates of the centre of mass of the system be
are placed on a plane as shown in figure. If the co-ordinates of the centre of mass of the system be  then the values of
then the values of  and
and  are respectively
are respectively

physics-General
physics-
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block ' A ' pulling it away from the other block 'B' as shown in figure at t=0. Extension of the spring is  at time t.
at time t.
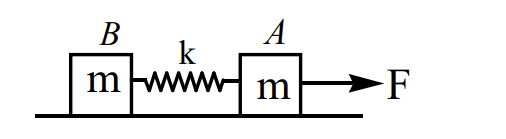 Displacement of the centre of mass at time t is
Displacement of the centre of mass at time t is
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block ' A ' pulling it away from the other block 'B' as shown in figure at t=0. Extension of the spring is  at time t.
at time t.
 Displacement of the centre of mass at time t is
Displacement of the centre of mass at time t is
physics-General
physics-
Two identical blocks of length L are piled on top of the other on a table as shown in the figure. The maximum distance S the top brick can overhang the table with the system still balanced, is

Two identical blocks of length L are piled on top of the other on a table as shown in the figure. The maximum distance S the top brick can overhang the table with the system still balanced, is

physics-General
physics-
A long, thin, inextensible and very flexible uniform wire is lying on the rough horizontal floor. One end of the wire is bent back and then pulled backwards with constant velocity V such that, at any instant of time, the moving part of the wire always remains just above the part of the wire which is still at rest at that instant on the floor as shown in diagram. If the wire has unit length and unit mass then,

A long, thin, inextensible and very flexible uniform wire is lying on the rough horizontal floor. One end of the wire is bent back and then pulled backwards with constant velocity V such that, at any instant of time, the moving part of the wire always remains just above the part of the wire which is still at rest at that instant on the floor as shown in diagram. If the wire has unit length and unit mass then,

physics-General
physics-
A smooth semicircular tube AB of radius r is fixed in a vertical plane and contains a heavy flexible chain of length  and weight per unit length 'w' as shown. Assuming a slight disturbance to start the chain. in motion, the velocity v with which it will emerge from the open end B of the tube is
and weight per unit length 'w' as shown. Assuming a slight disturbance to start the chain. in motion, the velocity v with which it will emerge from the open end B of the tube is

A smooth semicircular tube AB of radius r is fixed in a vertical plane and contains a heavy flexible chain of length  and weight per unit length 'w' as shown. Assuming a slight disturbance to start the chain. in motion, the velocity v with which it will emerge from the open end B of the tube is
and weight per unit length 'w' as shown. Assuming a slight disturbance to start the chain. in motion, the velocity v with which it will emerge from the open end B of the tube is

physics-General
physics-
Two persons of mass  and
and  are standing at the two ends A and B respectively of a trolley of mass M as shown When both the persons jump simultaneously with same speed then:
are standing at the two ends A and B respectively of a trolley of mass M as shown When both the persons jump simultaneously with same speed then:

Two persons of mass  and
and  are standing at the two ends A and B respectively of a trolley of mass M as shown When both the persons jump simultaneously with same speed then:
are standing at the two ends A and B respectively of a trolley of mass M as shown When both the persons jump simultaneously with same speed then:

physics-General
physics-
From the previous question in the reference frame attached to the center f inertia, the total kinetic energy of the two particles is
From the previous question in the reference frame attached to the center f inertia, the total kinetic energy of the two particles is
physics-General
physics-
A closed system consists of two particles of masses  and
and  which move at right angles to each other with velocities
which move at right angles to each other with velocities  and
and  . In the reference frame attached to the center of inertia, the magnitude of momentum of each particle is
. In the reference frame attached to the center of inertia, the magnitude of momentum of each particle is
A closed system consists of two particles of masses  and
and  which move at right angles to each other with velocities
which move at right angles to each other with velocities  and
and  . In the reference frame attached to the center of inertia, the magnitude of momentum of each particle is
. In the reference frame attached to the center of inertia, the magnitude of momentum of each particle is
physics-General
physics-
A man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform, with what velocity relative to the ice does the platform recoil?

A man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform, with what velocity relative to the ice does the platform recoil?

physics-General
physics-
A boy having a mass of M kg stands at one end A of a boat of length dm at rest. The boy walks to the other end B of the boat with a velocity u relative to the boat. What is the velocity of the boat? Friction exists between the feet of the boy and the surface of the boat. But the friction between the boat and the water surface may be neglected. Mass of the boat is 4 m

A boy having a mass of M kg stands at one end A of a boat of length dm at rest. The boy walks to the other end B of the boat with a velocity u relative to the boat. What is the velocity of the boat? Friction exists between the feet of the boy and the surface of the boat. But the friction between the boat and the water surface may be neglected. Mass of the boat is 4 m

physics-General
physics-
A equilateral triangular, square and circular plates of same thickness and made up of different materials are arranged is shown in figure.
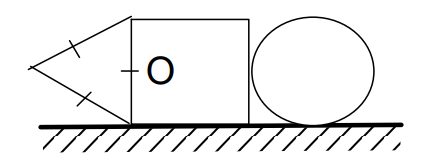 The ratio of their respective densities are
The ratio of their respective densities are  . The centre of mass of the arrangement lies
. The centre of mass of the arrangement lies
A equilateral triangular, square and circular plates of same thickness and made up of different materials are arranged is shown in figure.
 The ratio of their respective densities are
The ratio of their respective densities are  . The centre of mass of the arrangement lies
. The centre of mass of the arrangement lies
physics-General
physics-
The centre of mass of a triangular lamina of uniform density of height h is

The centre of mass of a triangular lamina of uniform density of height h is

physics-General
physics-
A semi-circular plate of radius R has density  , where
, where  is the distance from centre. The position of centre of mass from 0 is
is the distance from centre. The position of centre of mass from 0 is

A semi-circular plate of radius R has density  , where
, where  is the distance from centre. The position of centre of mass from 0 is
is the distance from centre. The position of centre of mass from 0 is

physics-General
physics-
A semi-circular plate with cavity having inner radius R and outer radius 2R with uniform density is a shown. The centre of mass of the thin plate is at

A semi-circular plate with cavity having inner radius R and outer radius 2R with uniform density is a shown. The centre of mass of the thin plate is at

physics-General



