Physics
General
Easy
Question
There is a prism with refractive index equal to 
and the refracting angle equal to 
. One of the refracting surfaces of the prism is polished. A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is.........
The correct answer is:
Related Questions to study
physics
The minimum angle of deviation of a prism of refractive index 1.732 is equal to its refracting angle. What is the angle of prism?
The minimum angle of deviation of a prism of refractive index 1.732 is equal to its refracting angle. What is the angle of prism?
physicsGeneral
physics
An equilateral prism deviates a ray through for two angles of incidence differing by 
. What is the nof the prism?
An equilateral prism deviates a ray through for two angles of incidence differing by . What is the nof the prism?
physicsGeneral
physics
The minimum deviation produced by a glass prism of angle is . If the velocity of light in vaccum is 
. Then what is the velocity of light in glass in m/s ?
The minimum deviation produced by a glass prism of angle is . If the velocity of light in vaccum is . Then what is the velocity of light in glass in m/s ?
physicsGeneral
physics-
Two identical parallel plate capacitors are placed in series and connected to a constant voltage source of 
volt. If one of the capacitor is completely immersed in a liquid of dielectric constant 
, then the potential difference between the plates of the other capacitor will change to
Two identical parallel plate capacitors are placed in series and connected to a constant voltage source of volt. If one of the capacitor is completely immersed in a liquid of dielectric constant , then the potential difference between the plates of the other capacitor will change to
physics-General
physics
Angle of prism is A and its one surface is silvered. Light rays falling at an angle at incidence 2 A on first surface return back through the same path after suffering reflection at second silvered surface What is the refractive index of material?
Angle of prism is A and its one surface is silvered. Light rays falling at an angle at incidence 2 A on first surface return back through the same path after suffering reflection at second silvered surface What is the refractive index of material?
physicsGeneral
physics
A light ray is incident perpendicular to one face of 
prism and is totally internally reflected at the glass-air interface. If the angle of reflection is . We conclude that the refractive index....
.
A light ray is incident perpendicular to one face of prism and is totally internally reflected at the glass-air interface. If the angle of reflection is . We conclude that the refractive index....
.
physicsGeneral
biology
The below diagram is a duct system of liver, gall bladder and pancreas. Write the names of ducts from A to D
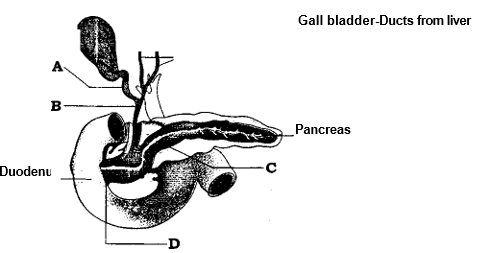
The below diagram is a duct system of liver, gall bladder and pancreas. Write the names of ducts from A to D
biologyGeneral
physics
A ray falls on a prism ABC(AB=BC) and travels as shown in the figure. The minimum refractive, index of the prism material should be.
A ray falls on a prism ABC(AB=BC) and travels as shown in the figure. The minimum refractive, index of the prism material should be.
physicsGeneral
physics
Two parallel light rays are incident at one surface of a prism of refractive index as shown in figure. What is the angle between the rays as they emerge ?
Two parallel light rays are incident at one surface of a prism of refractive index as shown in figure. What is the angle between the rays as they emerge ?
physicsGeneral
physics
An object is placed at a distance of 
the from a convex lens the image will be ...
An object is placed at a distance of the from a convex lens the image will be ...
physicsGeneral
physics
A concave mirror of focal length produces an images n times the size of the object. If the image is real then What is the distance of the object from the mirror?
A concave mirror of focal length produces an images n times the size of the object. If the image is real then What is the distance of the object from the mirror?
physicsGeneral
physics
A short linear object of length L lies on the axis of a spherical mirror of focal length of fat a distance u from the mirror. Its image has an axial length L ' equal to
A short linear object of length L lies on the axis of a spherical mirror of focal length of fat a distance u from the mirror. Its image has an axial length L ' equal to
physicsGeneral
physics
Which of the following graphs is the magnifications of a real image against the distance from the focus of a concave mirror?
Which of the following graphs is the magnifications of a real image against the distance from the focus of a concave mirror?
physicsGeneral
physics
A spherical mirror forms an erect image three times the linear size of the object. If the distance between the object and the image is 80 cm , What is the focal length of the mirror
A spherical mirror forms an erect image three times the linear size of the object. If the distance between the object and the image is 80 cm , What is the focal length of the mirror
physicsGeneral
physics
The distance between object and the screen is D . Real images of an object are formed on the screen two positions of a lens seperated by a distance d. What will be the ratio between the sizes of two images?
The distance between object and the screen is D . Real images of an object are formed on the screen two positions of a lens seperated by a distance d. What will be the ratio between the sizes of two images?
physicsGeneral
