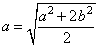Botany-
General
Easy
Question
If there are exactly two points on the ellipse  whose distance from its centre is same and is equal to
whose distance from its centre is same and is equal to  then eccentricity of the ellipse is
then eccentricity of the ellipse is
The correct answer is:

Related Questions to study
botany-
Tangent at any point  of ellipse
of ellipse  is drawn. Eccentric
is drawn. Eccentric
angle of ‘ P’ is  If
If  is the foot of perpendicular from centre
is the foot of perpendicular from centre  to this tangent then
to this tangent then  is
is
Tangent at any point  of ellipse
of ellipse  is drawn. Eccentric
is drawn. Eccentric
angle of ‘ P’ is  If
If  is the foot of perpendicular from centre
is the foot of perpendicular from centre  to this tangent then
to this tangent then  is
is
botany-General
botany-
If the curve  subtends as obtuse angle at the point
subtends as obtuse angle at the point  ,
, then a possible value of
then a possible value of  is
is
If the curve  subtends as obtuse angle at the point
subtends as obtuse angle at the point  ,
, then a possible value of
then a possible value of  is
is
botany-General
botany-
Let  . A point P in the XY-plane varies in such a way that perimeter of
. A point P in the XY-plane varies in such a way that perimeter of  is 16. Then the maximum area of
is 16. Then the maximum area of  is
is
Let  . A point P in the XY-plane varies in such a way that perimeter of
. A point P in the XY-plane varies in such a way that perimeter of  is 16. Then the maximum area of
is 16. Then the maximum area of  is
is
botany-General
botany-
 are points on the ellipse
are points on the ellipse  such that
such that  is a chord through the point
is a chord through the point  If
If  then length of chord
then length of chord  is
is
 are points on the ellipse
are points on the ellipse  such that
such that  is a chord through the point
is a chord through the point  If
If  then length of chord
then length of chord  is
is
botany-General
botany-
If  is a decreasing function for all
is a decreasing function for all  and
and  then the range of K so that the equation
then the range of K so that the equation  represents an ellipse whose major axis is the X-axis is
represents an ellipse whose major axis is the X-axis is
If  is a decreasing function for all
is a decreasing function for all  and
and  then the range of K so that the equation
then the range of K so that the equation  represents an ellipse whose major axis is the X-axis is
represents an ellipse whose major axis is the X-axis is
botany-General
botany-
From the focus  of the ellipse
of the ellipse  a ray of light is sent which makes angle
a ray of light is sent which makes angle  with the positive direction of X-axis upon reacting the ellipse the ray is reflected from it. Slope of the reflected ray is
with the positive direction of X-axis upon reacting the ellipse the ray is reflected from it. Slope of the reflected ray is
From the focus  of the ellipse
of the ellipse  a ray of light is sent which makes angle
a ray of light is sent which makes angle  with the positive direction of X-axis upon reacting the ellipse the ray is reflected from it. Slope of the reflected ray is
with the positive direction of X-axis upon reacting the ellipse the ray is reflected from it. Slope of the reflected ray is
botany-General
botany-
If the tangent at Point P to the ellipse 16x2 + 11y2 = 256 is also the tangent to the circle x2 + y2 - 2x = 15, then the eccentric angle of point P is
If the tangent at Point P to the ellipse 16x2 + 11y2 = 256 is also the tangent to the circle x2 + y2 - 2x = 15, then the eccentric angle of point P is
botany-General
botany-
If the curve x2 + 3y2 = 9 subtends an obtuse angle at the point (2a, a), then a possible value of a2 is
If the curve x2 + 3y2 = 9 subtends an obtuse angle at the point (2a, a), then a possible value of a2 is
botany-General
biology
The protective covering over radical during the germination of seeds is
The protective covering over radical during the germination of seeds is
biologyGeneral
Physics-
Determine the potential at point B, assuming point A to be at zero potential
<img src="https://mycourses.turito.com/tokenpluginfile.php/c161933dbfaab094c54655ab71e9b8f0/1/question/questiontext/869608/1/201040/Picture9.jpeg" alt="" width="160" height="108"
Determine the potential at point B, assuming point A to be at zero potential
<img src="https://mycourses.turito.com/tokenpluginfile.php/c161933dbfaab094c54655ab71e9b8f0/1/question/questiontext/869608/1/201040/Picture9.jpeg" alt="" width="160" height="108"
Physics-General
maths-
The domain of the function  is
is
The domain of the function  is
is
maths-General
Biology
Which region is responsible for origin of rhizoids in 
Which region is responsible for origin of rhizoids in 
BiologyGeneral
Biology
Winged pollen grains are found in
Winged pollen grains are found in
BiologyGeneral
Biology
The members of Chlorophyceae are usually green due to the dominance of pigments
The members of Chlorophyceae are usually green due to the dominance of pigments
BiologyGeneral
Biology
Select the correct statements.
Select the correct statements.
BiologyGeneral