Maths-
General
Easy
Question
=
- 0
- 1/4
- 3/4
- 5/4
Hint:
In the question we will start simplification with the formula 
then we will further solve it using some algebraic formula and some trigonometric identities like 
The correct answer is: 5/4
Related Questions to study
Maths-
If 
d then the minimum value of 
is equal to (where is variable)
If d then the minimum value of is equal to (where is variable)
Maths-General
biology
and 
then 
=
and then =
biologyGeneral
Maths-
Maths-General
Maths-
If 
then 
=
If then =
Maths-General
Maths-
The maximum value of the expression 
where 
and x are real numbers is
The maximum value of the expression
where and x are real numbers is
Maths-General
Maths-
If 
and 
then 
on multiplying equation 1 and 2,
If and then
Maths-General
on multiplying equation 1 and 2,
Maths-
The maximum value of 
under the restrictions 
and 
is
Given,
The maximum value of under the restrictions and is
Maths-General
Given,
Maths-
Let 
be two sets. Then
Given two sets
Let be two sets. Then
Maths-General
Given two sets
Maths-
If 
then 
is
If then is
Maths-General
physics-
A long cylindrical tube carries a highly polished piston and has a side opening. A tuning fork of frequency n is sounded at the sound heard by the listener charges if the piston is moves in or out. At a particular position of the piston is moved through a distance of 9 cm, the intensity of sound becomes minimum, if the speed of sound is 360 m/s, the value of n is
When piston moves a distance
, path difference change by 2 xs.
the path difference between maxima and consecutive minima=
∴
Or
λ=4x=4×9 cm=36cm=0.36m
, path difference change by 2 xs.the path difference between maxima and consecutive minima=∴
Or
λ=4x=4×9 cm=36cm=0.36m
A long cylindrical tube carries a highly polished piston and has a side opening. A tuning fork of frequency n is sounded at the sound heard by the listener charges if the piston is moves in or out. At a particular position of the piston is moved through a distance of 9 cm, the intensity of sound becomes minimum, if the speed of sound is 360 m/s, the value of n is
physics-General
When piston moves a distance, path difference change by 2 xs.
the path difference between maxima and consecutive minima=
∴
Or
λ=4x=4×9 cm=36cm=0.36m
, path difference change by 2 xs.the path difference between maxima and consecutive minima=∴
Or
λ=4x=4×9 cm=36cm=0.36m
Maths-
The value of 
The value of
Maths-General
Maths-
For any real 
, the maximum value of 
is
As cos is a decreasing function and sin is an increasing function so the function is maximum when =
.
So, the maximum value of = 
is maximum when =.So, the maximum value of
= For any real , the maximum value of is
Maths-General
As cos is a decreasing function and sin is an increasing function so the function is maximum when =.
So, the maximum value of =
is maximum when =.So, the maximum value of
= chemistry-
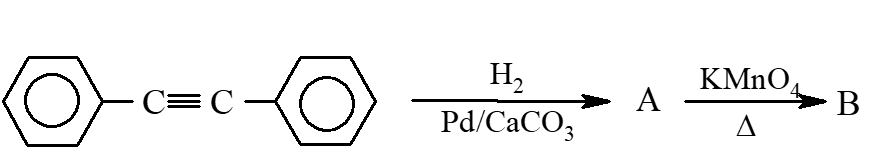Identify A and B
With H2 / pd / CaCO3 - is addition of ‘H’ know is oxidizing agent
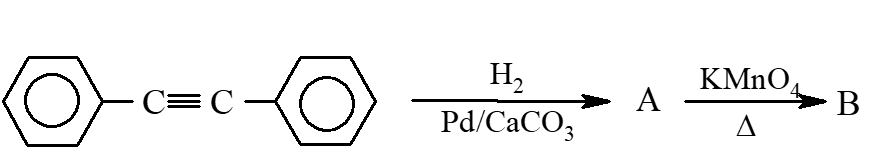Identify A and B
chemistry-General
With H2 / pd / CaCO3 - is addition of ‘H’ know is oxidizing agent
Maths-
If 
then sin (A-B) =
GIVEN-
√2 cos A = cos B + cos3 B..... equation 1
∴ cos A = 1/√2 (cos B + cos3 B) ........ (Dividing both sides by √2)
TO FIND-
Sin (A - B)
SOLUTION-
We know that-
Sin (A - B) = (Sin A * Cos B) - (Cos A * Sin B)
∴ Sin (A - B) = [1/√2 (sin B - sin3 B) * cos B] - [1/√2 (cos B + cos3 B) * sin B] ...... (From Equations i & ii)
∴ Sin (A - B) = [1/√2 * (sin B Cos B - sin3 B Cos B)] - [1/√2 * (sin B cos B + cos3 B * sin B)]
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - (1/√2 sin B cos B + 1/√2 cos3 B * sin B)
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin3 B Cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin B Cos B (sin2 B +cos2 B)
= -1/2√2 sin2B
Now squaring and adding equation 1 and 2 we get
√2 cos A = cos B + cos3 B..... equation 1
∴ cos A = 1/√2 (cos B + cos3 B) ........ (Dividing both sides by √2)
√2 sin A = sin B - sin3 B..... equation 2
∴ sin A = 1/√2 (sin B - sin3 B) ........ (Dividing both sides by √2)TO FIND-
Sin (A - B)
SOLUTION-
We know that-
Sin (A - B) = (Sin A * Cos B) - (Cos A * Sin B)
∴ Sin (A - B) = [1/√2 (sin B - sin3 B) * cos B] - [1/√2 (cos B + cos3 B) * sin B] ...... (From Equations i & ii)
∴ Sin (A - B) = [1/√2 * (sin B Cos B - sin3 B Cos B)] - [1/√2 * (sin B cos B + cos3 B * sin B)]
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - (1/√2 sin B cos B + 1/√2 cos3 B * sin B)
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin3 B Cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin B Cos B (sin2 B +cos2 B)
= -1/2√2 sin2B
Now squaring and adding equation 1 and 2 we get
If then sin (A-B) =
Maths-General
GIVEN-
√2 cos A = cos B + cos3 B..... equation 1
∴ cos A = 1/√2 (cos B + cos3 B) ........ (Dividing both sides by √2)
TO FIND-
Sin (A - B)
SOLUTION-
We know that-
Sin (A - B) = (Sin A * Cos B) - (Cos A * Sin B)
∴ Sin (A - B) = [1/√2 (sin B - sin3 B) * cos B] - [1/√2 (cos B + cos3 B) * sin B] ...... (From Equations i & ii)
∴ Sin (A - B) = [1/√2 * (sin B Cos B - sin3 B Cos B)] - [1/√2 * (sin B cos B + cos3 B * sin B)]
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - (1/√2 sin B cos B + 1/√2 cos3 B * sin B)
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin3 B Cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin B Cos B (sin2 B +cos2 B)
= -1/2√2 sin2B
Now squaring and adding equation 1 and 2 we get
√2 cos A = cos B + cos3 B..... equation 1
∴ cos A = 1/√2 (cos B + cos3 B) ........ (Dividing both sides by √2)
√2 sin A = sin B - sin3 B..... equation 2
∴ sin A = 1/√2 (sin B - sin3 B) ........ (Dividing both sides by √2)TO FIND-
Sin (A - B)
SOLUTION-
We know that-
Sin (A - B) = (Sin A * Cos B) - (Cos A * Sin B)
∴ Sin (A - B) = [1/√2 (sin B - sin3 B) * cos B] - [1/√2 (cos B + cos3 B) * sin B] ...... (From Equations i & ii)
∴ Sin (A - B) = [1/√2 * (sin B Cos B - sin3 B Cos B)] - [1/√2 * (sin B cos B + cos3 B * sin B)]
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - (1/√2 sin B cos B + 1/√2 cos3 B * sin B)
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = 1/√2 sin B Cos B - 1/√2 sin3 B Cos B - 1/√2 sin B cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin3 B Cos B - 1/√2 cos3 B * sin B
∴ Sin (A - B) = -1/√2 sin B Cos B (sin2 B +cos2 B)
= -1/2√2 sin2B
Now squaring and adding equation 1 and 2 we get