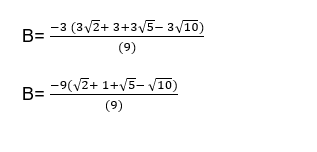Question
 , where
, where  and
and  is
is
- a negative integer
- a prime integer
- a positive integer
- an even–natural

In this question, we have to find the. Where the value of A and B is given A = √1 + √2 + √5- √10And B= . To solve this question, solve B, rationalize it find the value B then find the
. To solve this question, solve B, rationalize it find the value B then find the  .
.
The correct answer is: a positive integer
In this question, we have to find the . Here Solve first B. In B, rationalize it means multiply it denominator by sign change in both numerator and denominator
Related Questions to study
Statement 1:The equivalence point refers the condition where equivalents of one species react with same number of equivalent of other species.
Statement 2:The end point of titration is exactly equal to equivalence point
Statement 1:The equivalence point refers the condition where equivalents of one species react with same number of equivalent of other species.
Statement 2:The end point of titration is exactly equal to equivalence point
If and
are the roots of the equation
then the value of
equals
If and
are the roots of the equation
then the value of
equals
Statement 1:Iodimetric titration are redox titrations.
Statement 2:The iodine solution acts as an oxidant to reduce the reductant
Statement 1:Iodimetric titration are redox titrations.
Statement 2:The iodine solution acts as an oxidant to reduce the reductant
Statement 1:Diisopropyl ketone on reaction with isopropyl magnesium bromide followed by hydrolysis gives alcohol
Statement 2:Grignard reagent acts as a reducing agent
Statement 1:Diisopropyl ketone on reaction with isopropyl magnesium bromide followed by hydrolysis gives alcohol
Statement 2:Grignard reagent acts as a reducing agent
The first noble gas compound obtained was:
The first noble gas compound obtained was:
Given that and
then value of
equals –
These four basic properties all follow directly from the fact that logs are exponents.
logb(xy) = logbx + logby.
logb(x/y) = logbx - logby.
logb(xn) = n logbx.
logbx = logax / logab.
Given that and
then value of
equals –
These four basic properties all follow directly from the fact that logs are exponents.
logb(xy) = logbx + logby.
logb(x/y) = logbx - logby.
logb(xn) = n logbx.
logbx = logax / logab.
Statement 1:Change in colour of acidic solution of potassium dichromate by breath is used to test drunk drivers.
Statement 2:Change in colour is due to the complexation of alcohol with potassium dichromate.
Statement 1:Change in colour of acidic solution of potassium dichromate by breath is used to test drunk drivers.
Statement 2:Change in colour is due to the complexation of alcohol with potassium dichromate.
Total number of solutions of sin{x} = cos{x}, where {.} denotes the fractional part, in [0, 2] is equal to
In this question, we have to find the number of solutions. Here we have fractional part of x. It is {x} and {x}= x-[x]. The {x} is always belongs to 0 to 1.
Total number of solutions of sin{x} = cos{x}, where {.} denotes the fractional part, in [0, 2] is equal to
In this question, we have to find the number of solutions. Here we have fractional part of x. It is {x} and {x}= x-[x]. The {x} is always belongs to 0 to 1.
Statement 1:If a strong acid is added to a solution of potassium chromate it changes itscolour from yellow to orange.
Statement 2:The colour change is due to the oxidation of potassium chromate.
Statement 1:If a strong acid is added to a solution of potassium chromate it changes itscolour from yellow to orange.
Statement 2:The colour change is due to the oxidation of potassium chromate.
Total number of solutions of the equation 3x + 2 tan x = in x
[0, 2
] is equal to
In this question, we use the graph of tanx . The intersection is the total number of solutions of this equation. The graph region is [ 0, 2π ].
Total number of solutions of the equation 3x + 2 tan x = in x
[0, 2
] is equal to
In this question, we use the graph of tanx . The intersection is the total number of solutions of this equation. The graph region is [ 0, 2π ].
The number of sigma bonds in  is:
is:
The number of sigma bonds in  is:
is:
Statement 1:Oxidation number of Ni in is zero.
Statement 2:Nickel is bonded to neutral ligand carbonyl.
Statement 1:Oxidation number of Ni in is zero.
Statement 2:Nickel is bonded to neutral ligand carbonyl.
Suppose equation is f(x) – g(x) = 0 of f(x) = g(x) = y say, then draw the graphs of y = f(x) and y = g(x). If graph of y = f(x) and y = g(x) cuts at one, two, three, ...., no points, then number of solutions are one, two, three, ...., zero respectively.
The number of solutions of sin x = is
In this question, we have drawn the graph. The number of intersections of both function fx and gx are the number solutions. Draw the graph carefully and find the intersection points.
Suppose equation is f(x) – g(x) = 0 of f(x) = g(x) = y say, then draw the graphs of y = f(x) and y = g(x). If graph of y = f(x) and y = g(x) cuts at one, two, three, ...., no points, then number of solutions are one, two, three, ...., zero respectively.
The number of solutions of sin x = is
In this question, we have drawn the graph. The number of intersections of both function fx and gx are the number solutions. Draw the graph carefully and find the intersection points.
The first noble gas compound obtained was:
The first noble gas compound obtained was: