Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

Assertion (A) : 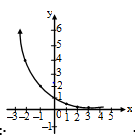Graph of $open curly brackets left parenthesis x comma y right parenthesis divided by y equals 2 to the power of negative x end exponent text and end text x comma y element of R close curly brackets$
Reason (R) : In the expression a^m/n, where a, m, n × J⁺, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.

If both (A) and (R) are true, and (R) is the correct explanation of (A) .
If both (A) and (R) are true but (R) is not the correct explanation of (A) .
If (A) is true but (R) is false.
If (A) is false but (R) is true.

The correct answer is: If (A) is false but (R) is true.

Related Questions to study

Assertion: The period of $f left parenthesis x right parenthesis equals s i n invisible function application 2 x c o s invisible function application left square bracket 2 x right square bracket minus c o s invisible function application 2 x s i n invisible function application left square bracket 2 x right square bracket$ is 1/2.
Reason: The period of x – [x] is 1.

Assertion: The period of $f left parenthesis x right parenthesis equals s i n invisible function application 2 x c o s invisible function application left square bracket 2 x right square bracket minus c o s invisible function application 2 x s i n invisible function application left square bracket 2 x right square bracket$ is 1/2.
Reason: The period of x – [x] is 1.

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Assertion: The function defined by $f left parenthesis x right parenthesis equals x to the power of 3 end exponent plus a x to the power of 2 end exponent plus b x plus c$ is invertible if and only if $a to the power of 2 end exponent less or equal than 3 b$ .
Reason: A function is invertible if and only if it is one-to-one and onto function.

Assertion: The function defined by $f left parenthesis x right parenthesis equals x to the power of 3 end exponent plus a x to the power of 2 end exponent plus b x plus c$ is invertible if and only if $a to the power of 2 end exponent less or equal than 3 b$ .
Reason: A function is invertible if and only if it is one-to-one and onto function.

parallel

Assertion : $f left parenthesis x right parenthesis equals s g n left parenthesis x minus vertical line x vertical line right parenthesis$ can never become positive.
Reason : f(x) = sgn x is always a positive function.

Assertion : $f left parenthesis x right parenthesis equals s g n left parenthesis x minus vertical line x vertical line right parenthesis$ can never become positive.
Reason : f(x) = sgn x is always a positive function.

If f (x) = $open curly brackets table row cell e to the power of cos invisible function application x end exponent end cell cell sin invisible function application x text for end text vertical line x vertical line less or equal than 2 end cell row cell text 2, end text end cell cell text otherwise end text end cell end table comma text then end text not stretchy integral subscript text -2 end text end subscript superscript 3 end superscript f left parenthesis x right parenthesis d x equals close$

If f (x) = $open curly brackets table row cell e to the power of cos invisible function application x end exponent end cell cell sin invisible function application x text for end text vertical line x vertical line less or equal than 2 end cell row cell text 2, end text end cell cell text otherwise end text end cell end table comma text then end text not stretchy integral subscript text -2 end text end subscript superscript 3 end superscript f left parenthesis x right parenthesis d x equals close$

The value of the integral $not stretchy integral subscript e to the power of negative 1 end exponent end subscript superscript e to the power of 2 end exponent end superscript open vertical bar fraction numerator log subscript e end subscript invisible function application blank x over denominator x end fraction close vertical bar$ dx is :

The value of the integral $not stretchy integral subscript e to the power of negative 1 end exponent end subscript superscript e to the power of 2 end exponent end superscript open vertical bar fraction numerator log subscript e end subscript invisible function application blank x over denominator x end fraction close vertical bar$ dx is :

parallel

Assertion : Let $f colon R minus left curly bracket 1 , 2 comma 3 right curly bracket rightwards arrow R$ be a function defined by f(x) = $fraction numerator 1 over denominator x minus 1 end fraction plus fraction numerator 2 over denominator x minus 2 end fraction plus fraction numerator 3 over denominator x minus 3 end fraction$ . Then f is many-one function.
Reason : If either $f apostrophe left parenthesis x right parenthesis greater than 0$ or $f to the power of apostrophe left parenthesis x right parenthesis less than 0 comma for all x element of$ domain of f, then y = f(x) is one-one function.</span

Assertion : Let $f colon R minus left curly bracket 1 , 2 comma 3 right curly bracket rightwards arrow R$ be a function defined by f(x) = $fraction numerator 1 over denominator x minus 1 end fraction plus fraction numerator 2 over denominator x minus 2 end fraction plus fraction numerator 3 over denominator x minus 3 end fraction$ . Then f is many-one function.
Reason : If either $f apostrophe left parenthesis x right parenthesis greater than 0$ or $f to the power of apostrophe left parenthesis x right parenthesis less than 0 comma for all x element of$ domain of f, then y = f(x) is one-one function.</span

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Function $f colon Z rightwards arrow Z comma$ f(x) = 2x + 1 is-

Function $f colon Z rightwards arrow Z comma$ f(x) = 2x + 1 is-

parallel

If f(x) is an even function and $f to the power of apostrophe left parenthesis x right parenthesis$ Exist for all 'X' then f'(1)+f'(-1) is-

If f(x) is an even function and $f to the power of apostrophe left parenthesis x right parenthesis$ Exist for all 'X' then f'(1)+f'(-1) is-

In two separate collisions, the coefficient of restitutions and are in the ratio 3:1.In the first collision the relative velocity of approach is twice the relative velocity of separation ,then the ratio between relative velocity of approach and the relative velocity of separation in the second collision is

In two separate collisions, the coefficient of restitutions and are in the ratio 3:1.In the first collision the relative velocity of approach is twice the relative velocity of separation ,then the ratio between relative velocity of approach and the relative velocity of separation in the second collision is

physics-General

Suppose $f left parenthesis x right parenthesis equals left parenthesis x plus 1 right parenthesis squared$ for $x greater or equal than negative 1$ . If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals–

Suppose $f left parenthesis x right parenthesis equals left parenthesis x plus 1 right parenthesis squared$ for $x greater or equal than negative 1$ . If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals–

parallel

A spotlight installed in the ground shines on a wall. A woman stands between the light and the wall casting a shadow on the wall. How are the rate at which she walks away from the light and rate at which her shadow grows related ?

A spotlight installed in the ground shines on a wall. A woman stands between the light and the wall casting a shadow on the wall. How are the rate at which she walks away from the light and rate at which her shadow grows related ?

If reaction is R and coefficient of friction is $blank mu$ , what is work done against friction in moving a body by distance d?

If reaction is R and coefficient of friction is $blank mu$ , what is work done against friction in moving a body by distance d?

physics-General

The force $F$ acting on a particle moving in a straight line is shown in figure. What is the work done by the force on the particle in the 1^st meter of the trajectory

The force $F$ acting on a particle moving in a straight line is shown in figure. What is the work done by the force on the particle in the 1^st meter of the trajectory

physics-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.