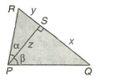
Question
Let 
then 
Hint:
In GP Sum of infinite terms: S∞ = a / (1 - r) when |r| < 1 and the sum is NOT defined when |r| ≥ 1.
The correct answer is:
Given :
To Find : ?
Detailed Solution
Related Questions to study
Let 
be A.P and 
be in H.P If 
and 
the 
Let be A.P and be in H.P If and the
The work done by a force acting on a body is as shown in the graph. what is the total work done in covering an initial distance of 15 m?
The work done by a force acting on a body is as shown in the graph. what is the total work done in covering an initial distance of 15 m?
A 8 kg mass moves along x - axis. Its accelerations as a function of its position is shown in the figure. What is the total work done on the mass by the force as the mass moves from x=0 to x=6 cm ?
A 8 kg mass moves along x - axis. Its accelerations as a function of its position is shown in the figure. What is the total work done on the mass by the force as the mass moves from x=0 to x=6 cm ?
If A and G are A.M and G.M between two positive numbers a and b are connected by the relation A+G=a-b then the numbers are in the ratio
We have to be careful while solving quadratic equation questions as there are chances of mistakes with the signs while finding the roots. Sometimes the students try to use factorisation methods to solve the quadratic equation, but in this type of questions, it is not recommended at all. Always try to use the quadratic formula for solving. You can also remember the statement to be proved, given in the question as a property for two positive numbers.
If A and G are A.M and G.M between two positive numbers a and b are connected by the relation A+G=a-b then the numbers are in the ratio
We have to be careful while solving quadratic equation questions as there are chances of mistakes with the signs while finding the roots. Sometimes the students try to use factorisation methods to solve the quadratic equation, but in this type of questions, it is not recommended at all. Always try to use the quadratic formula for solving. You can also remember the statement to be proved, given in the question as a property for two positive numbers.
If 
where a<1, b<1 then
If where a<1, b<1 then
If l, m, n are the 
terms of a G.P which are +ve, then 
If l, m, n are the terms of a G.P which are +ve, then
The relationship between force and position is shown in the figure given (in one dimensional case) calculate the work done by the force in displacing a body from x=0 cm to x=5 cm
The relationship between force and position is shown in the figure given (in one dimensional case) calculate the work done by the force in displacing a body from x=0 cm to x=5 cm
Fifth term of G.P is 2 The product of its first nine terms is
Here note that the fifth term is having fourth power of 2 and not fifth power. We need not to find all nine terms separately; only finding the product is enough because that product will then be written in the form of the term that is known. Terms in a G.P. are having a common ratio in between. That’s why the power of r is increasing as the terms are increasing.
Fifth term of G.P is 2 The product of its first nine terms is
Here note that the fifth term is having fourth power of 2 and not fifth power. We need not to find all nine terms separately; only finding the product is enough because that product will then be written in the form of the term that is known. Terms in a G.P. are having a common ratio in between. That’s why the power of r is increasing as the terms are increasing.
, 
are in
are in A.P with common difference 
then sind 
terms] 
digits )=
as shown in figure given that 
, then the value of 
is
at position A is just sufficient to make it reach the point B. The angle 
at which the speed of the bob is half of that at A, satisfies
