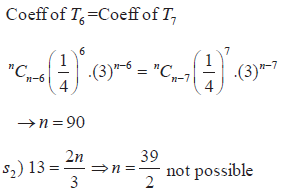Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

S1: If the coefficients of $x to the power of 6 end exponent$ and $x to the power of 7 end exponent$ in the expansion of $left parenthesis fraction numerator x over denominator 4 end fraction plus 3 right parenthesis to the power of n end exponent$ are equal, then the number ofdivisors ofn is 12.
S2: If the expansion of $left parenthesis x to the power of 2 end exponent plus fraction numerator 2 over denominator x end fraction right parenthesis to the power of n end exponent$ for positive integer n has 13 ^th term independent of x Then the sum of divisors of $n$ is 39.

Only $S_{1}$ is true
Only $S_{2}$ is true
Both $S_{1}$ and $S_{2}$ are true
Neither $S_{1}$ nor $S_{2}$ is true

The correct answer is: Both $S subscript 1 end subscript$ and $S subscript 2 end subscript$ are true

Related Questions to study

I Three consecutive binomial coefficients cannot be in GP.
II Three consecutive binomial coefficients cannot be in A.P.
Which of the above statement is correct?

I Three consecutive binomial coefficients cannot be in GP.
II Three consecutive binomial coefficients cannot be in A.P.
Which of the above statement is correct?

I The no of distinct terms in the expansion of $left parenthesis x subscript 1 end subscript plus x subscript 2 end subscript plus horizontal ellipsis. plus x subscript n end subscript right parenthesis to the power of 3 end exponent$ is $n plus 2 c subscript 3 end subscript$
II The no of irrational terms in the expansion $left parenthesis 2 to the power of 1 divided by 5 end exponent plus 3 to the power of 1 divided by 10 end exponent right parenthesis to the power of 55 end exponent$ is 55

I The no of distinct terms in the expansion of $left parenthesis x subscript 1 end subscript plus x subscript 2 end subscript plus horizontal ellipsis. plus x subscript n end subscript right parenthesis to the power of 3 end exponent$ is $n plus 2 c subscript 3 end subscript$
II The no of irrational terms in the expansion $left parenthesis 2 to the power of 1 divided by 5 end exponent plus 3 to the power of 1 divided by 10 end exponent right parenthesis to the power of 55 end exponent$ is 55

If $left parenthesis 3 plus x to the power of 2008 end exponent plus x to the power of 2009 end exponent right parenthesis to the power of 2010 end exponent$ $equals a subscript 0 end subscript plus a subscript 1 end subscript x plus a subscript 2 end subscript x to the power of 2 end exponent plus$ $plus a subscript n end subscript x to the power of n end exponent$ then $a subscript 0 end subscript minus fraction numerator a subscript 1 end subscript over denominator 2 end fraction minus fraction numerator a subscript 2 end subscript over denominator 2 end fraction plus a subscript 3 end subscript minus fraction numerator a subscript 4 end subscript over denominator 2 end fraction minus fraction numerator a subscript 5 end subscript over denominator 2 end fraction plus a subscript 6 end subscript$

If $left parenthesis 3 plus x to the power of 2008 end exponent plus x to the power of 2009 end exponent right parenthesis to the power of 2010 end exponent$ $equals a subscript 0 end subscript plus a subscript 1 end subscript x plus a subscript 2 end subscript x to the power of 2 end exponent plus$ $plus a subscript n end subscript x to the power of n end exponent$ then $a subscript 0 end subscript minus fraction numerator a subscript 1 end subscript over denominator 2 end fraction minus fraction numerator a subscript 2 end subscript over denominator 2 end fraction plus a subscript 3 end subscript minus fraction numerator a subscript 4 end subscript over denominator 2 end fraction minus fraction numerator a subscript 5 end subscript over denominator 2 end fraction plus a subscript 6 end subscript$

parallel

If $left curly bracket x right curly bracket$ denotes fractional part of $x$ then $left curly bracket fraction numerator 2 to the power of 2003 end exponent over denominator 17 end fraction right curly bracket equals$

If $left curly bracket x right curly bracket$ denotes fractional part of $x$ then $left curly bracket fraction numerator 2 to the power of 2003 end exponent over denominator 17 end fraction right curly bracket equals$

$404 C subscript 4 end subscript minus C subscript 4 end subscript. C subscript 1 end subscript plus 2024 minus 1014 equals$

$404 C subscript 4 end subscript minus C subscript 4 end subscript. C subscript 1 end subscript plus 2024 minus 1014 equals$

The number of rational terms in the expansion of $left parenthesis 1 plus square root of 2 plus root index 3 of 3 end root right parenthesis to the power of 6 end exponent$ is

The number of rational terms in the expansion of $left parenthesis 1 plus square root of 2 plus root index 3 of 3 end root right parenthesis to the power of 6 end exponent$ is

parallel

If $2 to the power of 2006 end exponent minus 2006$ divided by 7, the remainder is

If $2 to the power of 2006 end exponent minus 2006$ divided by 7, the remainder is

The remainder when $2 3 to the power of 23 end exponent$ is divided by 53 is

The remainder when $2 3 to the power of 23 end exponent$ is divided by 53 is

If $C subscript r end subscript equals 32 C subscript r end subscript$ , then $not stretchy sum subscript r equals 0 end subscript superscript 5 end superscript C subscript 6 r end subscript equals$

If $C subscript r end subscript equals 32 C subscript r end subscript$ , then $not stretchy sum subscript r equals 0 end subscript superscript 5 end superscript C subscript 6 r end subscript equals$

parallel

$bullet$ If $C subscript r end subscript equals to the power of 30 end exponent C subscript r end subscript$ , then $C subscript 0 end subscript plus C subscript 4 end subscript plus C subscript 8 end subscript plus$ $plus C subscript 28 end subscript equals$

$bullet$ If $C subscript r end subscript equals to the power of 30 end exponent C subscript r end subscript$ , then $C subscript 0 end subscript plus C subscript 4 end subscript plus C subscript 8 end subscript plus$ $plus C subscript 28 end subscript equals$

A particle goes from point A to B. Its displacement is X and pathlength is y. So $x over y$

A particle goes from point A to B. Its displacement is X and pathlength is y. So $x over y$

A car goes from one end to the other end of a semicircular path of diameter ' d '. Find the ratio between path length and displacement.

A car goes from one end to the other end of a semicircular path of diameter ' d '. Find the ratio between path length and displacement.

parallel

A particle moves from A to P and then it moves from P to B as shown in the figure. Find path length and displacement.

A particle moves from A to P and then it moves from P to B as shown in the figure. Find path length and displacement.

If the thickness of the wire is doubled, then the breaking force in the above question will be

If the thickness of the wire is doubled, then the breaking force in the above question will be

physics-General

The Young’s modulus of the material of a wire is $2 cross times 10 to the power of 10 end exponent N m to the power of negative 2 end exponent.$ If the elongation strain is $1 percent sign$ , then the energy stored in the wire per unit volume in $J m blank to the power of negative 3 end exponent$ is

The Young’s modulus of the material of a wire is $2 cross times 10 to the power of 10 end exponent N m to the power of negative 2 end exponent.$ If the elongation strain is $1 percent sign$ , then the energy stored in the wire per unit volume in $J m blank to the power of negative 3 end exponent$ is

physics-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.