Maths-
General
Easy
Question
The condition that the line 
x + my = n may be a normal to the ellipse 
+ 
= 1 is
= 1
= 1
- = 2
- None of these
= 1
= 1
= 2
The correct answer is: = 1
Related Questions to study
Physics-
Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a (
). (g is acceleration due to gravity). Normal reaction (in N) acting on block A.
Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity). Normal reaction (in N) acting on block A.
Physics-General
physics-
Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity) Normal reaction (in N) acting on block B is
Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity) Normal reaction (in N) acting on block B is
physics-General
physics-
A light inextensible string connects a block of mass m and top of wedge of mass M. The string is parallel to inclined surface and the inclined surface makes an angle 
with horizontal as shown in the figure. All surfaces are smooth. Now a constant horizontal force of minimum magnitude F is applied to wedge towards right such that the normal reaction on block exerted by wedge just becomes zero. The magnitude of acceleration of wedge is
A light inextensible string connects a block of mass m and top of wedge of mass M. The string is parallel to inclined surface and the inclined surface makes an angle with horizontal as shown in the figure. All surfaces are smooth. Now a constant horizontal force of minimum magnitude F is applied to wedge towards right such that the normal reaction on block exerted by wedge just becomes zero. The magnitude of acceleration of wedge is
physics-General
maths-
The vector 
which is perpendicular to (2,-3,1) and (1,-2,3) and which satisfies the condition 
The vector which is perpendicular to (2,-3,1) and (1,-2,3) and which satisfies the condition
maths-General
Maths-
Let f : R → R be a differentiable function satisfying f (x) = f (x – y) f (y) " x, y Î R and f ¢ (0) = a, f ¢ (2) = b then f ¢ (-2) is
Let f : R → R be a differentiable function satisfying f (x) = f (x – y) f (y) " x, y Î R and f ¢ (0) = a, f ¢ (2) = b then f ¢ (-2) is
Maths-General
physics-
Four identical metal butterflies are hanging from a light string of length 
at equally placed points as shown in the figure . The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle 
and 
is given by
Four identical metal butterflies are hanging from a light string of length at equally placed points as shown in the figure . The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle and is given by
physics-General
physics-
Initially the spring is undeformed. Now the force 'F' is applied to 'B' as shown in the figure . When the displacement of 'B' w.r.t 'A' is 'x' towards right in some time then the relative acceleration of 'B' w.r.t. 'A' at that moment is:
Initially the spring is undeformed. Now the force 'F' is applied to 'B' as shown in the figure . When the displacement of 'B' w.r.t 'A' is 'x' towards right in some time then the relative acceleration of 'B' w.r.t. 'A' at that moment is:
physics-General
physics-
Mass m shown in the figure is in equilibrium. If it is displaced further by x and released find its acceleration just after it is released. Take pulleys to be light & smooth and strings light.
Mass m shown in the figure is in equilibrium. If it is displaced further by x and released find its acceleration just after it is released. Take pulleys to be light & smooth and strings light.
physics-General
physics-
In the figure shown, the pulleys and strings are massless. The acceleration of the block of mass 4m just after the system is released from rest is 
In the figure shown, the pulleys and strings are massless. The acceleration of the block of mass 4m just after the system is released from rest is
physics-General
maths-
If S and 
are two foci of an ellipse 
+
= 1 
and P 
a point on it, then SP + P is equal to-
If S and are two foci of an ellipse += 1 and P a point on it, then SP + P is equal to-
maths-General
physics-
A cylinder rests in a supporting carriage as shown. The side AB of carriage makes an angle 
with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration 'a'. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be 
respectively. Neglect friction everywhere. Then as the magnitude of acceleration 'a ' of the carriage is increased, pick up the correct statement:
A cylinder rests in a supporting carriage as shown. The side AB of carriage makes an angle with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration 'a'. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be respectively. Neglect friction everywhere. Then as the magnitude of acceleration 'a ' of the carriage is increased, pick up the correct statement:
physics-General
physics-
In the figure shown, a person wants to raise a block lying on the ground to a height h. In both the cases if time required is same then in which case he has to exert more force. Assume pulleys and strings light.
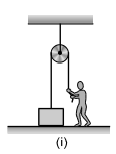
In the figure shown, a person wants to raise a block lying on the ground to a height h. In both the cases if time required is same then in which case he has to exert more force. Assume pulleys and strings light.
physics-General
physics-
A rod of length 
is moving such that its ends A and B move in contact with the horizontal floor and vertical wall respectively as shown in figure. O is the intersection point of the vertical wall and horizontal floor. The velocity vector of the centre of rod C is always directed along tangent drawn at C to the –
A rod of length is moving such that its ends A and B move in contact with the horizontal floor and vertical wall respectively as shown in figure. O is the intersection point of the vertical wall and horizontal floor. The velocity vector of the centre of rod C is always directed along tangent drawn at C to the –
physics-General
maths-
The orthogonal projection of 
on 
are unit vectors along three mutually perpendicular directions )
The orthogonal projection of on are unit vectors along three mutually perpendicular directions )
maths-General
maths-
If S and are foci and A be one and of minor axis of ellipse 
+
= 1, then area of 
is-
If S and are foci and A be one and of minor axis of ellipse += 1, then area of is-
maths-General
