Physics-
General
Easy
Question
A body of mass 
is moving with a uniform speed 
along a circle of radius 
, what is the average acceleration in going from 
to 
?
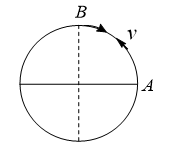
- None of these
The correct answer is:
Here, 
Change in velocity is going from to = 
Average acceleration 
Related Questions to study
Physics-
Figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to initial horizontal velocity component, highest first
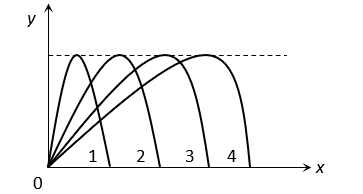
Figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to initial horizontal velocity component, highest first
Physics-General
physics-
A boy throws a cricket ball from the boundary to the wicket-keeper. If the frictional force due to air cannot be ignored, the forces acting on the ball at the position X are respected by
A boy throws a cricket ball from the boundary to the wicket-keeper. If the frictional force due to air cannot be ignored, the forces acting on the ball at the position X are respected by
physics-General
physics-
In a two dimensional motion of a particle, the particle moves from point , position vector 
. If the magnitudes of these vectors are respectively, 
=3 and 
and the angles they make with the 
-axis are 
and 15
, respectively, then find the magnitude of the displacement vector
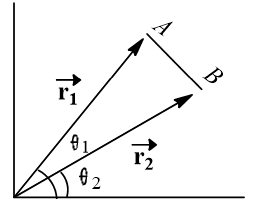
In a two dimensional motion of a particle, the particle moves from point , position vector . If the magnitudes of these vectors are respectively, =3 and and the angles they make with the -axis are and 15, respectively, then find the magnitude of the displacement vector
physics-General
Physics-
A particle is moving on a circular path of radius with uniform velocity . The change in velocity when the particle moves from 
to
is
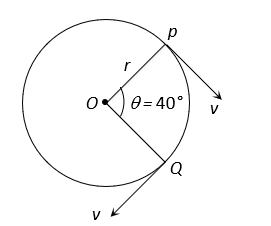
A particle is moving on a circular path of radius with uniform velocity . The change in velocity when the particle moves from tois
Physics-General
Physics-
From an inclined plane two particles are projected with same speed at same angle 
, one up and other down the plane as shown in figure, which of the following statements is/are correct?
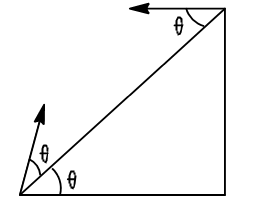
From an inclined plane two particles are projected with same speed at same angle , one up and other down the plane as shown in figure, which of the following statements is/are correct?
Physics-General
physics-
A string of length 
is fixed at one end and carries a mass 
at the other end. The string makes 
revolutions per 
around the vertical axis through the fixed end as shown in figure , then tension in the string is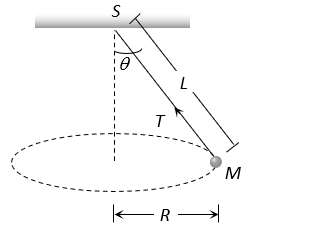
A string of length is fixed at one end and carries a mass at the other end. The string makes revolutions per around the vertical axis through the fixed end as shown in figure , then tension in the string is
physics-General
physics-
A piece of wire is bent in the shape of a parabola 
-axis vertical) with a bead of mass on it. The bead can side on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the -axis with a constant acceleration 
. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the 
-axis is
A piece of wire is bent in the shape of a parabola -axis vertical) with a bead of mass on it. The bead can side on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the -axis with a constant acceleration . The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the -axis is
physics-General
physics-
A frictionless track 
ends in a circular loop of radius 
figure. A body slides down the track from point which is at a height 
cm. Maximum value of 
for the body to successfully complete the loop is
A frictionless track ends in a circular loop of radius figure. A body slides down the track from point which is at a height cm. Maximum value of for the body to successfully complete the loop is
physics-General
Physics-
The resultant of a system of forces shown in figure is a force of 10 N parallel to given forces through , where 
equals
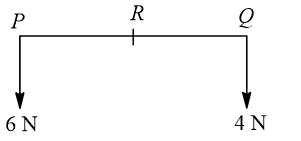
The resultant of a system of forces shown in figure is a force of 10 N parallel to given forces through , where equals
Physics-General
physics-
The time taken by the projectile to reach from to is 
then the distance 
is equal to
The time taken by the projectile to reach from to is then the distance is equal to
physics-General
physics-
Two identical discs of same radius are rotating about their axes in opposite directions with the same constant angular speed 
. The discs are in the same horizontal plane. At time 
, the points 
and 
are facing each other as shown in figure. The relative speed between the two points and is 
as function of times best represented by
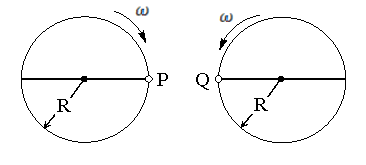
Two identical discs of same radius are rotating about their axes in opposite directions with the same constant angular speed . The discs are in the same horizontal plane. At time , the points and are facing each other as shown in figure. The relative speed between the two points and is as function of times best represented by
physics-General
Physics-
A small body of mass slides down from the top of a hemisphere of radius . The surface of block and hemisphere are frictionless. The height at which the body lose contact with the surface of the sphere is
A small body of mass slides down from the top of a hemisphere of radius . The surface of block and hemisphere are frictionless. The height at which the body lose contact with the surface of the sphere is
Physics-General
Physics-
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position are 
The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
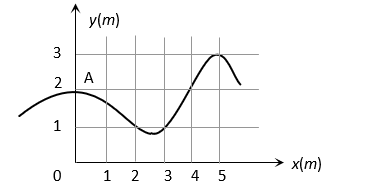
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position are The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
Physics-General
physics-
A point mass is suspended from a light thread of length 
fixed at
, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are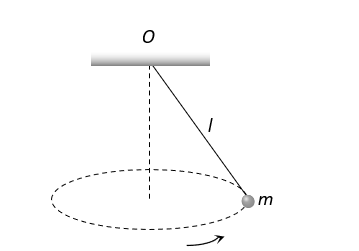
A point mass is suspended from a light thread of length fixed at, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are
physics-General
physics-
A particle is projected from a point with velocity 
at an angle of 
with horizontal as shown in figure. It strikes the plane 
at right angles. The velocity of the particle at the time of collision is
A particle is projected from a point with velocity at an angle of with horizontal as shown in figure. It strikes the plane at right angles. The velocity of the particle at the time of collision is
physics-General
