Physics-
General
Easy
Question
A small particle of mass  is projected at an angle
is projected at an angle  with the
with the  -axis with an initial velocity
-axis with an initial velocity  in the
in the  -
- plane as shown in the figure.
plane as shown in the figure.  the angular momentum of the particle is
the angular momentum of the particle is

The correct answer is: 
Related Questions to study
physics-
The figures represent three cases of a ray passing through a prism of angle A. The case corresponding to minimum deviation is

The figures represent three cases of a ray passing through a prism of angle A. The case corresponding to minimum deviation is

physics-General
Maths-
If the normal at the point  to the ellipse
to the ellipse  intersects it again at the point
intersects it again at the point  , then
, then  is
is
If the normal at the point  to the ellipse
to the ellipse  intersects it again at the point
intersects it again at the point  , then
, then  is
is
Maths-General
physics-
A fighter plane enters inside the enemy territory, at time  with velocity
with velocity  and moves horizontally with constant acceleration
and moves horizontally with constant acceleration  (see figure). An enemy tank at the border, spot the plane and fire shots at an angle
(see figure). An enemy tank at the border, spot the plane and fire shots at an angle  with the horizontal and with velocity
with the horizontal and with velocity  . At what altitude
. At what altitude  of the plane it can be hit by the shot?
of the plane it can be hit by the shot?

A fighter plane enters inside the enemy territory, at time  with velocity
with velocity  and moves horizontally with constant acceleration
and moves horizontally with constant acceleration  (see figure). An enemy tank at the border, spot the plane and fire shots at an angle
(see figure). An enemy tank at the border, spot the plane and fire shots at an angle  with the horizontal and with velocity
with the horizontal and with velocity  . At what altitude
. At what altitude  of the plane it can be hit by the shot?
of the plane it can be hit by the shot?

physics-General
physics-
A light ray is incident by grazing one of the face of a prism and after refraction ray does not emerge out, what should be the angle of prism while critical angle is C</em
A light ray is incident by grazing one of the face of a prism and after refraction ray does not emerge out, what should be the angle of prism while critical angle is C</em
physics-General
physics-
A particle of mass  is rotating in a horizontal circle of radius
is rotating in a horizontal circle of radius  and is attached to a hanging mass
and is attached to a hanging mass  as shown in the figure. The speed of rotation required by the mass
as shown in the figure. The speed of rotation required by the mass  keep
keep  steady is
steady is

A particle of mass  is rotating in a horizontal circle of radius
is rotating in a horizontal circle of radius  and is attached to a hanging mass
and is attached to a hanging mass  as shown in the figure. The speed of rotation required by the mass
as shown in the figure. The speed of rotation required by the mass  keep
keep  steady is
steady is

physics-General
physics-
Figure shows the variation of the stopping potential (V0) with the frequency (v) of theincident radiations for two different photosensitive material M1 and M2 .What are the values of work functions for M1 and M2 respectively

Figure shows the variation of the stopping potential (V0) with the frequency (v) of theincident radiations for two different photosensitive material M1 and M2 .What are the values of work functions for M1 and M2 respectively

physics-General
physics-
The respective angles of the flint and crown glass prisms are  and A. They are to be used for dispersion without deviation, then the ratio of their angles
and A. They are to be used for dispersion without deviation, then the ratio of their angles  will be
will be
The respective angles of the flint and crown glass prisms are  and A. They are to be used for dispersion without deviation, then the ratio of their angles
and A. They are to be used for dispersion without deviation, then the ratio of their angles  will be
will be
physics-General
physics-
The two lines A and B shown in figure are the agraphs of the de Broglie wavelength l as function of  (V is the accelerating potential) for two particles having the same charge
(V is the accelerating potential) for two particles having the same charge 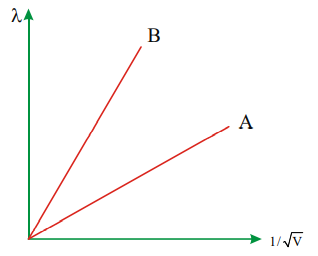
Which of the two represents the particle of heavier mass ?
The two lines A and B shown in figure are the agraphs of the de Broglie wavelength l as function of  (V is the accelerating potential) for two particles having the same charge
(V is the accelerating potential) for two particles having the same charge 
Which of the two represents the particle of heavier mass ?
physics-General
physics-
In a photoelectric experiment anode potential is plotted against plate current

In a photoelectric experiment anode potential is plotted against plate current

physics-General
physics-
From an inclined plane two particles are projected with same speed at same angle  , one up and other down the plane as shown in figure. Which of the following statements
, one up and other down the plane as shown in figure. Which of the following statements  is/are correct?
is/are correct?

From an inclined plane two particles are projected with same speed at same angle  , one up and other down the plane as shown in figure. Which of the following statements
, one up and other down the plane as shown in figure. Which of the following statements  is/are correct?
is/are correct?

physics-General
Physics-
Two particles 1 and 2 are projected with same speed  as shown in figure. Particle 2 is on the ground and particle 1 is at a height
as shown in figure. Particle 2 is on the ground and particle 1 is at a height  from the ground and at a horizontal distance
from the ground and at a horizontal distance  from particle 2. If a graph is plotted between
from particle 2. If a graph is plotted between  and
and  for the condition of collision of the two then (
for the condition of collision of the two then ( on
on  -axis and
-axis and  on
on  -axis
-axis

Two particles 1 and 2 are projected with same speed  as shown in figure. Particle 2 is on the ground and particle 1 is at a height
as shown in figure. Particle 2 is on the ground and particle 1 is at a height  from the ground and at a horizontal distance
from the ground and at a horizontal distance  from particle 2. If a graph is plotted between
from particle 2. If a graph is plotted between  and
and  for the condition of collision of the two then (
for the condition of collision of the two then ( on
on  -axis and
-axis and  on
on  -axis
-axis

Physics-General
physics-
a) Name the experiment for which the adjacent graph, showing the variation of intensity of scattered electrons with the angle of scatter ing (q) was obtained.
b) Also name the important hypothesis that was confirmed by this experiment

a) Name the experiment for which the adjacent graph, showing the variation of intensity of scattered electrons with the angle of scatter ing (q) was obtained.
b) Also name the important hypothesis that was confirmed by this experiment

physics-General
physics-
Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is  , then the ratio of tensions in the three sections of the string is
, then the ratio of tensions in the three sections of the string is

Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is  , then the ratio of tensions in the three sections of the string is
, then the ratio of tensions in the three sections of the string is

physics-General
physics-
A ball of mass kg is attached to the end of a string having length
kg is attached to the end of a string having length  0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is
0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is

A ball of mass kg is attached to the end of a string having length
kg is attached to the end of a string having length  0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is
0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is

physics-General
maths-
The ellipse  and the straight line y = mx + c intersect in real points only if
and the straight line y = mx + c intersect in real points only if
The ellipse  and the straight line y = mx + c intersect in real points only if
and the straight line y = mx + c intersect in real points only if
maths-General



