Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

Two insulating plates are both uniformly charged in such a way that the potential difference between them is $V subscript 2 end subscript minus V subscript 1 end subscript equals 20$ V. ( $i e$ , plate 2 is at a higher potential). The plates are separated by $d equals 0.1$ m and can be treated as infinitely large. An electron is released from rest on the inner surface of plate 1. What is its speed when it hits plate 2? (e=1.6 $cross times 10 to the power of negative 19 end exponent C comma m subscript 0 end subscript equals 9.11 cross times 10 to the power of negative 31 end exponent k g right parenthesis$

$2.65 \times 10^{6} {m s}^{- 1}$
$7.02 \times 10^{12} {m s}^{- 1}$
$1.87 \times 10^{6} {m s}^{- 1}$
$32 \times 10^{- 19} {m s}^{- 1}$

The correct answer is: $2.65 cross times 10 to the power of 6 end exponent m s to the power of negative 1 end exponent$

Since $V subscript 2 end subscript greater than V subscript 1 end subscript comma$ so electric field will point from plate 2 to plate 1.
The electron will experience an electric force, opposite to the direction of electric field, and hence move towards the plate 2.

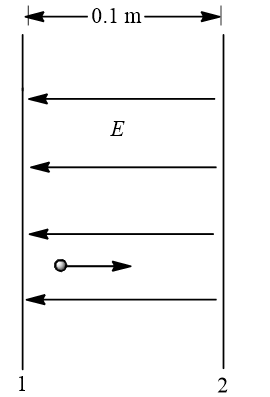
Use work-energy theorem to find speed of electron when it strikes the plate 2.
$fraction numerator m subscript e end subscript v to the power of 2 end exponent over denominator 2 end fraction minus 0 equals e left parenthesis V subscript 2 end subscript minus V subscript 1 end subscript right parenthesis$
Where $v$ is the required speed.
$therefore blank fraction numerator 9.11 cross times 10 to the power of negative 31 end exponent over denominator 2 end fraction v to the power of 2 end exponent equals 1.6 cross times 10 to the power of negative 19 end exponent cross times 20$
$rightwards double arrow blank v equals blank square root of fraction numerator 1.6 cross times 10 to the power of negative 19 end exponent cross times 40 over denominator 9.11 cross times 10 to the power of negative 31 end exponent end fraction end root equals 2.65 cross times 10 to the power of 6 end exponent m s to the power of negative 1 end exponent$

Related Questions to study

Calculate the force ' ' F that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height 4m. Radius of the wheel is 1m and its mass is $open parentheses g equals 10 m s to the power of negative 2 end exponent close parentheses$

Calculate the force ' ' F that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height 4m. Radius of the wheel is 1m and its mass is $open parentheses g equals 10 m s to the power of negative 2 end exponent close parentheses$

physics-General

A wheel of radius ‘r’ and mass ‘m’ stands in front of a step of height 'h’ The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is

A wheel of radius ‘r’ and mass ‘m’ stands in front of a step of height 'h’ The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is

physics-General

The order of differential equation is $open parentheses fraction numerator d squared y over denominator d x squared end fraction close parentheses cubed equals open parentheses 1 plus fraction numerator d y over denominator d x end fraction close parentheses to the power of 1 divided by 2 end exponent$

The order of differential equation is $open parentheses fraction numerator d squared y over denominator d x squared end fraction close parentheses cubed equals open parentheses 1 plus fraction numerator d y over denominator d x end fraction close parentheses to the power of 1 divided by 2 end exponent$

parallel

Two condensers, one of capacity $C$ and the other of capacity $fraction numerator C over denominator 2 end fraction$ , are connected to a $V$ volt battery , as shown. The work done in charging fully both the condensers is

Two condensers, one of capacity $C$ and the other of capacity $fraction numerator C over denominator 2 end fraction$ , are connected to a $V$ volt battery , as shown. The work done in charging fully both the condensers is

physics-General

A cubical block of side ‘L’ rests on a rough horizontal surface with coefficient of friction ‘m’ A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

A cubical block of side ‘L’ rests on a rough horizontal surface with coefficient of friction ‘m’ A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

physics-General

If the time period of a pendulum is 1 sec, then what is the length of the pendulum at point of intersection of l-T and $l minus T to the power of 2 end exponent$ graph

If the time period of a pendulum is 1 sec, then what is the length of the pendulum at point of intersection of l-T and $l minus T to the power of 2 end exponent$ graph

physics-General

parallel

Order and degree of differential equation $fraction numerator d squared y over denominator d x squared end fraction equals open square brackets y plus open parentheses fraction numerator d y over denominator d x end fraction close parentheses squared close square brackets to the power of 1 divided by 4 end exponent$ are

Order and degree of differential equation $fraction numerator d squared y over denominator d x squared end fraction equals open square brackets y plus open parentheses fraction numerator d y over denominator d x end fraction close parentheses squared close square brackets to the power of 1 divided by 4 end exponent$ are

The solution of $x squared fraction numerator d y over denominator d x end fraction minus x y equals 1 plus cos space y over x$ is

The solution of $x squared fraction numerator d y over denominator d x end fraction minus x y equals 1 plus cos space y over x$ is

For the given figure, calculate zero correction.

For the given figure, calculate zero correction.

physics-General

parallel

Three capacitors $C subscript 1 end subscript comma C subscript 2 end subscript a n d C subscript 3 end subscript$ are connected as shown in the figure to a battery of $V$ volt. If the capacitor $C subscript 3 end subscript$ breaks down electrically the change in total charge on the combination of capacitors is

Three capacitors $C subscript 1 end subscript comma C subscript 2 end subscript a n d C subscript 3 end subscript$ are connected as shown in the figure to a battery of $V$ volt. If the capacitor $C subscript 3 end subscript$ breaks down electrically the change in total charge on the combination of capacitors is

physics-General

The charge deposited on $4 mu F$ capacitor the circuit is

The charge deposited on $4 mu F$ capacitor the circuit is

physics-General

If $y equals e to the power of negative x end exponent left parenthesis A cos space x plus B sin space x right parenthesis$ then y satisfies

If $y equals e to the power of negative x end exponent left parenthesis A cos space x plus B sin space x right parenthesis$ then y satisfies

parallel

In the figure, a proton moves a distance d in a uniform electric field E as shown in the figure. Does the electric field do a positive or negative work on the proton? Does the electric potential energy of the proton increase or decrease?

In the figure, a proton moves a distance d in a uniform electric field E as shown in the figure. Does the electric field do a positive or negative work on the proton? Does the electric potential energy of the proton increase or decrease?

physics-General

Solution of $fraction numerator d y over denominator d x end fraction equals e to the power of y plus x end exponent plus e to the power of y minus x end exponent$ is

Solution of $fraction numerator d y over denominator d x end fraction equals e to the power of y plus x end exponent plus e to the power of y minus x end exponent$ is

Two charges $q subscript 1 end subscript$ and $q subscript 2 end subscript$ are placed 30 cm apart, as shown in the figure. A third charge $q subscript 3 end subscript$ is moved along the arc of a circle of radius 40 cm from C to D. The change in the potential energy of the system is $fraction numerator q subscript 3 end subscript over denominator 4 pi epsilon subscript 0 end subscript end fraction k comma$ where k is

Two charges $q subscript 1 end subscript$ and $q subscript 2 end subscript$ are placed 30 cm apart, as shown in the figure. A third charge $q subscript 3 end subscript$ is moved along the arc of a circle of radius 40 cm from C to D. The change in the potential energy of the system is $fraction numerator q subscript 3 end subscript over denominator 4 pi epsilon subscript 0 end subscript end fraction k comma$ where k is

physics-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.