Chemistry-
General
Easy
Question
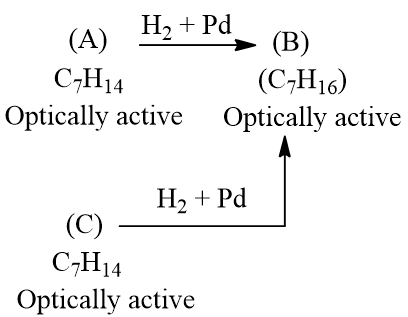
(A) and(C) are different compound s and rotate the plane-polarised light in the same direction, andboth are dextrorotatory. Both (A) and(C) do not show diastereomers, whichof the following statements are correct?
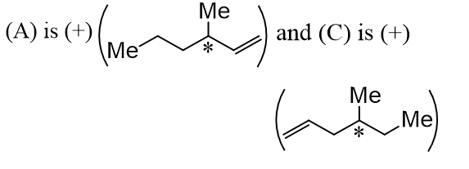
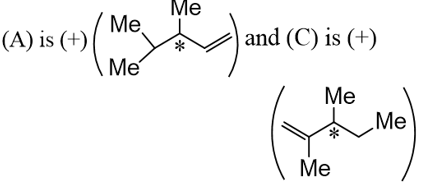
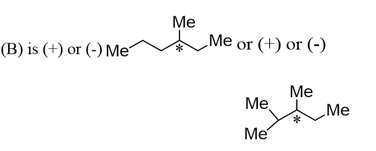
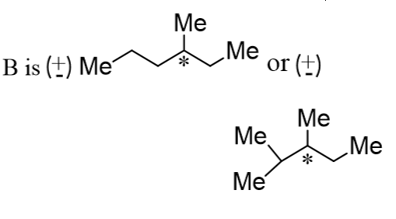
The correct answer is:
Related Questions to study
chemistry-
Which of the following dienes and dienophiles could be used to synthesise the following compound (A) ?
Which of the following dienes and dienophiles could be used to synthesise the following compound (A) ?
chemistry-General
Maths-
16 sin 
16 sin
Maths-General
physics-
Five conductors are meeting at a point x as shown in the figure. What is the value of current in fifth conductor?
Five conductors are meeting at a point x as shown in the figure. What is the value of current in fifth conductor?
physics-General
physics-
The figure shows a network of currents. The magnitude of current is shown here. The current I will be
The figure shows a network of currents. The magnitude of current is shown here. The current I will be
physics-General
physics-
The equivalent resistance between the terminals 
in the following circuit is
The equivalent resistance between the terminals in the following circuit is
physics-General
physics-
The equivalent resistance between points A and B of an infinite network of resistances, each of 1
, connected as shown is
The equivalent resistance between points A and B of an infinite network of resistances, each of 1, connected as shown is
physics-General
Maths-
The period of 
is
The period of is
Maths-General
Maths-
The period of 
is
The period of is
Maths-General
Maths-
Period of tan 4x+sec 4x is
Period of tan 4x+sec 4x is
Maths-General
Maths-
The cotangent function whose period 
is
The cotangent function whose period is
Maths-General
physics-
Thirteen resistances each of resistance R
are connected in the circuit as shown in the figure. The effective resistance between points A and B is
Thirteen resistances each of resistance R are connected in the circuit as shown in the figure. The effective resistance between points A and B is
physics-General
physics-
Six resistors, each of value 3 are connected as shown in the figure. A cell of emf 3V is connected across 
The effective resistance across 
and the current through the arm will be
Six resistors, each of value 3 are connected as shown in the figure. A cell of emf 3V is connected across The effective resistance across and the current through the arm will be
physics-General
physics-
In the circuit shown the value of I in ampere is
In the circuit shown the value of I in ampere is
physics-General
physics-
The given graph shows the variation of velocity with displacement. Which one of the graph given below correctly represents the variation of acceleration with displacement?
The given graph shows the variation of velocity with displacement. Which one of the graph given below correctly represents the variation of acceleration with displacement?
physics-General
physics-
The displacement-time graphs of two moving particles make angles of 
with the 
axis. The ratio of their velocities is
The displacement-time graphs of two moving particles make angles of with the axis. The ratio of their velocities is
physics-General
