Question
If  , then the intervals of values of
, then the intervals of values of  for which
for which  , is
, is
The correct answer is: 
Related Questions to study
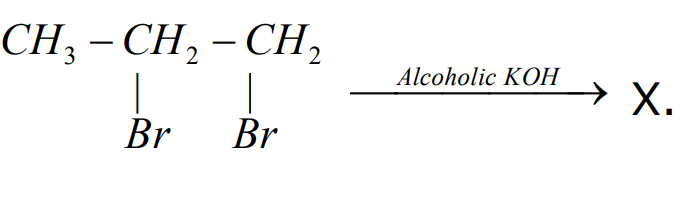 . X is an unsaturated gaseous hydrocarbon. Find X?
. X is an unsaturated gaseous hydrocarbon. Find X?
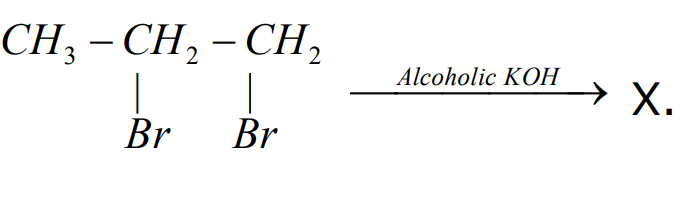 . X is an unsaturated gaseous hydrocarbon. Find X?
. X is an unsaturated gaseous hydrocarbon. Find X?
The eq. wt. of  in the reaction,
in the reaction,  is/are:
is/are:
The eq. wt. of  in the reaction,
in the reaction,  is/are:
is/are:
Which statement(s) is/are wrong?
Which statement(s) is/are wrong?
To solve a trigonometric inequation of the type sin x ≥ a where |a| ≤ 1, we take a hill of length 2 in the sine curve and write the solution within that hill. For the general solution, we add 2n
. For instance, to solve
, we take the hill
over which solution is
The general solution is
, n is any integer. Again to solve an inequation of the type sin x ≤ a, where |a| ≤ 1, we take a hollow of length 2
in the sine curve. (since on a hill, sinx ≤ a is satisfied over two intervals). Similarly cos x ≥ a or cosx ≤a, |a| ≤ 1 are solved.
Solution to the inequation must be
To solve a trigonometric inequation of the type sin x ≥ a where |a| ≤ 1, we take a hill of length 2 in the sine curve and write the solution within that hill. For the general solution, we add 2n
. For instance, to solve
, we take the hill
over which solution is
The general solution is
, n is any integer. Again to solve an inequation of the type sin x ≤ a, where |a| ≤ 1, we take a hollow of length 2
in the sine curve. (since on a hill, sinx ≤ a is satisfied over two intervals). Similarly cos x ≥ a or cosx ≤a, |a| ≤ 1 are solved.
Solution to the inequation must be
Which of the following compounds does not give halo form reaction?
Which of the following compounds does not give halo form reaction?
The oxidation number of carboxylic carbon atom in  is:
is:
The oxidation number of carboxylic carbon atom in  is:
is:
The oxidation number of carboxylic carbon atom in  is:
is:
The oxidation number of carboxylic carbon atom in  is:
is:
 The product (A) is:
The product (A) is:
 The product (A) is:
The product (A) is:
If  then
then  is always
is always
If  then
then  is always
is always
 The compound (A) is:
The compound (A) is:
 The compound (A) is:
The compound (A) is:
The oxidation number of C in  is:
is:
The oxidation number of C in  is:
is:
 has
has
In this question, we have to find the number of solution. In each quadrant tan value is different. Make two different case, one is where tan is positive ,[ 0 , π/2 ] U [π , 3 π/2 ] . And second case , tan is negative at [π/2 , π] U [3 π/2 , 2 π ] .
 has
has
In this question, we have to find the number of solution. In each quadrant tan value is different. Make two different case, one is where tan is positive ,[ 0 , π/2 ] U [π , 3 π/2 ] . And second case , tan is negative at [π/2 , π] U [3 π/2 , 2 π ] .
If  then for all real values of q
then for all real values of q
If  then for all real values of q
then for all real values of q
 The products (A) , (B) and (C) are:
The products (A) , (B) and (C) are:
 The products (A) , (B) and (C) are:
The products (A) , (B) and (C) are:
In the interval , the equation,
has
In the interval , the equation,
has



