Maths-

General

Easy

Question

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, adj A and A^–1

If both (A) and (R) are true, and (R) is the correct explanation of (A).
If both (A) and (R) are true but (R) is not the correct explanation of (A).
If (A) is true but (R) is false.
If (A) is false but (R) is true.

The correct answer is: If (A) is false but (R) is true.

The reason R is true since
AI = IA, AA^–1 = A^–1A = I, A|adj A| = |adj. A|A
But a matrix can commute with general order matrices which may be infinite in number.
Let B = $open square brackets table row a b row c d end table close square brackets$ be a matrix which commute with A then AB = BA
$not stretchy rightwards double arrow$ $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$ $open square brackets table row a b row c d end table close square brackets$ = $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
= $open square brackets table row cell a plus 2 c end cell cell b plus 2 d end cell row cell negative a minus c end cell cell negative b minus d end cell end table close square brackets$ = $open square brackets table row cell a minus b end cell cell 2 a minus b end cell row cell c minus d end cell cell 2 c minus d end cell end table close square brackets$
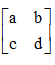
$not stretchy rightwards double arrow$ a + 2c = a – b, b + 2d = 2a – b, – a – c= c – d, – b – d = 2c – d
The above four relations are equivalent to only two independent relations
a – d = b, b + 2c = 0
If d = $lambda$ , then a = b + $lambda$ = –2c + $lambda$
Thus, $open square brackets table row cell lambda minus 2 c end cell cell negative 2 c end cell row c lambda end table close square brackets$ are all possible 2 × 2 matrices which commute with given matrix A = $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
$lambda$ and c being any arbitrary complex numbers. Thus assertion is therefore false.

Statement-I The equation $square root of 3 cos space x minus sin space x equals 2$ has exactly one solution in [0, 2 $straight pi$ ].
Statement-II For equations of type $a cos space theta plus b sin space theta equals c$ to have real solutions in $left square bracket 0 comma 2 pi right square bracket comma vertical line c vertical line less or equal than square root of a squared plus b squared end root$ should hold true.

In this question, we have to find the statements are the correct or not and statement 2 is correct explanation or not , is same like assertion and reason. Here, Start solving first Statement and try to prove it . Then solve the Statement-II . Remember cos a cosb -sin a sinb = cos ( a + b ) and sin a cosb + cosa sinb = sin( a+ b) .

Statement-I The equation $square root of 3 cos space x minus sin space x equals 2$ has exactly one solution in [0, 2 $straight pi$ ].
Statement-II For equations of type $a cos space theta plus b sin space theta equals c$ to have real solutions in $left square bracket 0 comma 2 pi right square bracket comma vertical line c vertical line less or equal than square root of a squared plus b squared end root$ should hold true.

Maths-General

General

maths-

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $straight A to the power of straight prime$ = det (– $straight A to the power of straight prime$ )

maths-General

General

maths-

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrix
$open square brackets table attributes columnalign center center columnspacing 1em end attributes row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, adj A and A^–1

maths-General

General

maths-

Consider the system of equationsx – 2y + 3z = –1–x + y – 2z = kx – 3y + 4z = 1
Assertion : The system of equations has no solution for k $not equal to$ 3.and
Reason : The determinant $open vertical bar table row 1 3 cell negative 1 end cell row cell negative 1 end cell cell negative 2 end cell k row 1 4 1 end table close vertical bar$ $not equal to$ 0, for k $not equal to$ 3.

maths-General

General

maths-

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c $not equal to$ 0
Reason : a² + b² + c² > ab + bc + ca if a, b, c are distinct

maths-General

General

maths-

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $A to the power of straight prime$ = det (– $A to the power of straight prime$ )

maths-General

General

maths-

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, Adj A and A^–1.

maths-General

General

maths-

Let a matrix A = $open square brackets table row 1 1 row 0 1 end table close square brackets$ & P = $open square brackets table row cell fraction numerator square root of 3 over denominator 2 end fraction end cell cell fraction numerator 1 over denominator 2 end fraction end cell row cell negative fraction numerator 1 over denominator 2 end fraction end cell cell fraction numerator square root of 3 over denominator 2 end fraction end cell end table close square brackets$ Q = PAP^T where P^T is transpose of matrix P. Find PT Q2005 P is

maths-General

General

maths-

Let A = $open square brackets table row 1 0 0 row 0 1 1 row 0 cell negative 2 end cell 4 end table close square brackets$ & I = $open square brackets table row 1 0 0 row 0 1 0 row 0 0 1 end table close square brackets$ and A–1 = $fraction numerator 1 over denominator 6 end fraction$ [A²+ cA + dI], find ordered pair (c, d) ?]

maths-General

General

maths-

$open square brackets table row alpha 2 row 2 alpha end table close square brackets$ = A & | A³ | = 125, then $alpha$ is -

maths-General

General

maths-

If A = $open square brackets table row alpha 0 row 1 1 end table close square brackets$ , B = $open square brackets table row 1 0 row 5 1 end table close square brackets$ and A² = B, then

maths-General

General

Maths-

Let A be a square matrix all of whose entries are integers. Then which one of the following is true ?

Maths-General

General

maths-

Let A = $open square brackets table row 5 cell 5 alpha end cell alpha row 0 alpha cell 5 alpha end cell row 0 0 5 end table close square brackets$ If |A2| = 25, then | $alpha$ | equals

maths-General

General

Maths-

Let A = $open parentheses table row 1 2 row 3 4 end table close parentheses$ and B = $open parentheses table row a 0 row 0 b end table close parentheses$ , a, b $element of$ N. Then

Maths-General

General

Maths-

If A and B are square matrices of size n × n such that A² – B² = (A – B) (A + B), then which of the following will be always true –

Maths-General

Have a query? Ask a Tutor!!

Can’t find what you’re looking for?

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, adj A and A^–1

If both (A) and (R) are true, and (R) is the correct explanation of (A).
If both (A) and (R) are true but (R) is not the correct explanation of (A).
If (A) is true but (R) is false.
If (A) is false but (R) is true.

The correct answer is: If (A) is false but (R) is true.

Related Questions to study

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $straight A to the power of straight prime$ = det (– $straight A to the power of straight prime$ )

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $straight A to the power of straight prime$ = det (– $straight A to the power of straight prime$ )

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c $not equal to$ 0
Reason : a² + b² + c² > ab + bc + ca if a, b, c are distinct

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c $not equal to$ 0
Reason : a² + b² + c² > ab + bc + ca if a, b, c are distinct

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $A to the power of straight prime$ = det (– $A to the power of straight prime$ )

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $A to the power of straight prime$ = det (– $A to the power of straight prime$ )

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, Adj A and A^–1.

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, Adj A and A^–1.

$open square brackets table row alpha 2 row 2 alpha end table close square brackets$ = A & | A³ | = 125, then $alpha$ is -

$open square brackets table row alpha 2 row 2 alpha end table close square brackets$ = A & | A³ | = 125, then $alpha$ is -

If A = $open square brackets table row alpha 0 row 1 1 end table close square brackets$ , B = $open square brackets table row 1 0 row 5 1 end table close square brackets$ and A² = B, then

If A = $open square brackets table row alpha 0 row 1 1 end table close square brackets$ , B = $open square brackets table row 1 0 row 5 1 end table close square brackets$ and A² = B, then

Let A be a square matrix all of whose entries are integers. Then which one of the following is true ?

Let A be a square matrix all of whose entries are integers. Then which one of the following is true ?

Let A = $open square brackets table row 5 cell 5 alpha end cell alpha row 0 alpha cell 5 alpha end cell row 0 0 5 end table close square brackets$ If |A2| = 25, then | $alpha$ | equals

Let A = $open square brackets table row 5 cell 5 alpha end cell alpha row 0 alpha cell 5 alpha end cell row 0 0 5 end table close square brackets$ If |A2| = 25, then | $alpha$ | equals

Let A = $open parentheses table row 1 2 row 3 4 end table close parentheses$ and B = $open parentheses table row a 0 row 0 b end table close parentheses$ , a, b $element of$ N. Then

Let A = $open parentheses table row 1 2 row 3 4 end table close parentheses$ and B = $open parentheses table row a 0 row 0 b end table close parentheses$ , a, b $element of$ N. Then

If A and B are square matrices of size n × n such that A² – B² = (A – B) (A + B), then which of the following will be always true –

If A and B are square matrices of size n × n such that A² – B² = (A – B) (A + B), then which of the following will be always true –

With Turito Academy.

With Turito Foundation.

Get an Expert Advice From Turito.

Turito Academy

With Turito Academy.

Test Prep

With Turito Foundation.

Courses

Quick Links

Follow Us at

Support

Download App

Courses

Quick Links

Have a query? Ask a Tutor!!

Can’t find what you’re looking for?

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrix Reason : If A is non-singular then it commutes with I, adj A and A–1

If both (A) and (R) are true, and (R) is the correct explanation of (A). If both (A) and (R) are true but (R) is not the correct explanation of (A). If (A) is true but (R) is false. If (A) is false but (R) is true.

The correct answer is: If (A) is false but (R) is true.

Related Questions to study

Statement-I The equation has exactly one solution in [0, 2].Statement-II For equations of type to have real solutions in should hold true.

Statement-I The equation has exactly one solution in [0, 2].Statement-II For equations of type to have real solutions in should hold true.

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.Reason : If A is square matrix then det A = det = det (–)

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.Reason : If A is square matrix then det A = det = det (–)

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrixReason : If A is non-singular then it commutes with I, adj A and A–1

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrixReason : If A is non-singular then it commutes with I, adj A and A–1

Consider the system of equationsx – 2y + 3z = –1–x + y – 2z = kx – 3y + 4z = 1Assertion : The system of equations has no solution for k 3.andReason : The determinant 0, for k 3.

Consider the system of equationsx – 2y + 3z = –1–x + y – 2z = kx – 3y + 4z = 1Assertion : The system of equations has no solution for k 3.andReason : The determinant 0, for k 3.

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c 0Reason : a2 + b2 + c2 > ab + bc + ca if a, b, c are distinct

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c 0Reason : a2 + b2 + c2 > ab + bc + ca if a, b, c are distinct

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.Reason : If A is square matrix then det A = det = det (–)

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.Reason : If A is square matrix then det A = det = det (–)

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix Reason : If A is non-singular then it commutes with I, Adj A and A–1.

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix Reason : If A is non-singular then it commutes with I, Adj A and A–1.

Let a matrix A = & P = Q = PAPT where PT is transpose of matrix P. Find PT Q2005 P is

Let a matrix A = & P = Q = PAPT where PT is transpose of matrix P. Find PT Q2005 P is

Let A = & I = and A–1 = [A2 + cA + dI], find ordered pair (c, d) ?]

Let A = & I = and A–1 = [A2 + cA + dI], find ordered pair (c, d) ?]

= A & | A3 | = 125, then is -

= A & | A3 | = 125, then is -

If A = , B = and A2 = B, then

If A = , B = and A2 = B, then

Let A be a square matrix all of whose entries are integers. Then which one of the following is true ?

Let A be a square matrix all of whose entries are integers. Then which one of the following is true ?

Let A = If |A2| = 25, then || equals

Let A = If |A2| = 25, then || equals

Let A = and B = , a, b N. Then

Let A = and B = , a, b N. Then

If A and B are square matrices of size n × n such that A2 – B2 = (A – B) (A + B), then which of the following will be always true –

If A and B are square matrices of size n × n such that A2 – B2 = (A – B) (A + B), then which of the following will be always true –

With Turito Academy.

With Turito Foundation.

Get an Expert Advice From Turito.

Turito Academy

With Turito Academy.

Test Prep

With Turito Foundation.

Courses

Quick Links

Assertion : There are only finitely many 2 × 2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, adj A and A^–1

If both (A) and (R) are true, and (R) is the correct explanation of (A).
If both (A) and (R) are true but (R) is not the correct explanation of (A).
If (A) is true but (R) is false.
If (A) is false but (R) is true.

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $straight A to the power of straight prime$ = det (– $straight A to the power of straight prime$ )

Assertion : If A is a skew symmetric matrix of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $straight A to the power of straight prime$ = det (– $straight A to the power of straight prime$ )

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c $not equal to$ 0
Reason : a² + b² + c² > ab + bc + ca if a, b, c are distinct

Assertion : If a, b, c are distinct and x, y, z are not all zero given that ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 then a + b + c $not equal to$ 0
Reason : a² + b² + c² > ab + bc + ca if a, b, c are distinct

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $A to the power of straight prime$ = det (– $A to the power of straight prime$ )

Assertion : If A is a skew symmetric of order 3 then its determinant should be zero.
Reason : If A is square matrix then det A = det $A to the power of straight prime$ = det (– $A to the power of straight prime$ )

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, Adj A and A^–1.

Assertion : There are only finitely many 2 ×2 matrices which commute with the matrix $open square brackets table row 1 2 row cell negative 1 end cell cell negative 1 end cell end table close square brackets$
Reason : If A is non-singular then it commutes with I, Adj A and A^–1.

$open square brackets table row alpha 2 row 2 alpha end table close square brackets$ = A & | A³ | = 125, then $alpha$ is -

$open square brackets table row alpha 2 row 2 alpha end table close square brackets$ = A & | A³ | = 125, then $alpha$ is -

If A = $open square brackets table row alpha 0 row 1 1 end table close square brackets$ , B = $open square brackets table row 1 0 row 5 1 end table close square brackets$ and A² = B, then

If A = $open square brackets table row alpha 0 row 1 1 end table close square brackets$ , B = $open square brackets table row 1 0 row 5 1 end table close square brackets$ and A² = B, then

Let A = $open square brackets table row 5 cell 5 alpha end cell alpha row 0 alpha cell 5 alpha end cell row 0 0 5 end table close square brackets$ If |A2| = 25, then | $alpha$ | equals

Let A = $open square brackets table row 5 cell 5 alpha end cell alpha row 0 alpha cell 5 alpha end cell row 0 0 5 end table close square brackets$ If |A2| = 25, then | $alpha$ | equals

Let A = $open parentheses table row 1 2 row 3 4 end table close parentheses$ and B = $open parentheses table row a 0 row 0 b end table close parentheses$ , a, b $element of$ N. Then

Let A = $open parentheses table row 1 2 row 3 4 end table close parentheses$ and B = $open parentheses table row a 0 row 0 b end table close parentheses$ , a, b $element of$ N. Then

If A and B are square matrices of size n × n such that A² – B² = (A – B) (A + B), then which of the following will be always true –

If A and B are square matrices of size n × n such that A² – B² = (A – B) (A + B), then which of the following will be always true –