Maths-
General
Easy
Question
If  , then at
, then at 
 is continuous and
is continuous and 
1 + = log 10 e , f ' 1 - = - log 10 e  is continuous and
is continuous and 
1 + = log 10 e , f ' 1 - = log 10 e  is continuous and
is continuous and 
1 - = log 10 e , f ' 1 + = - log 10 e - None of these
The correct answer is:  is continuous and
is continuous and 
As is evident from the graph of  that it is continuous but not differentiable at
that it is continuous but not differentiable at 
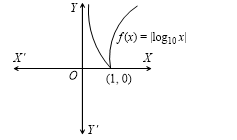
Now,







Related Questions to study
Maths-
If  then a + x =
then a + x =
If  then a + x =
then a + x =
Maths-General
chemistry-
Which of the following statements about the interstitial compounds is incorrect?
Which of the following statements about the interstitial compounds is incorrect?
chemistry-General
physics
Potential energy of a satellite having mass m and rotating at a height of 6.4 m from the surface of earth
m from the surface of earth
Potential energy of a satellite having mass m and rotating at a height of 6.4 m from the surface of earth
m from the surface of earth
physicsGeneral
Maths-
The slant height of a cone is fixed as 7 cm. If the rate of increase in its height is 0.3 cm/sec. Then the rate of increase in volume when the height is 4cm
The slant height of a cone is fixed as 7 cm. If the rate of increase in its height is 0.3 cm/sec. Then the rate of increase in volume when the height is 4cm
Maths-General
physics
A satellite with K.E. EK is revolving round the earth in a circular orbit. How much more K.E. should be given to it so that it may just escape into outer space?
A satellite with K.E. EK is revolving round the earth in a circular orbit. How much more K.E. should be given to it so that it may just escape into outer space?
physicsGeneral
Maths-
If A,B,C are the maximum velocities of the particles moving according to the law  respectively then the ascending order of A,B,C is
respectively then the ascending order of A,B,C is
If A,B,C are the maximum velocities of the particles moving according to the law  respectively then the ascending order of A,B,C is
respectively then the ascending order of A,B,C is
Maths-General
physics
A satellite moves around the earth in a circular orbit of radius r with speed v, If mass of the satellite is M, its total energy is
A satellite moves around the earth in a circular orbit of radius r with speed v, If mass of the satellite is M, its total energy is
physicsGeneral
chemistry-
Which one of the following d-block elements has half-filled penultimate d-subshell as well as half filled penultimate d-subshell as well as half filled valence s-subshell?
Which one of the following d-block elements has half-filled penultimate d-subshell as well as half filled penultimate d-subshell as well as half filled valence s-subshell?
chemistry-General
Maths-
A conical vessel of height 10ft and semivertical angle  is full of water. If empties in such away that the height at the water in the vessel is decreasing at a constant rate of 1ft/min. Then the rate at which the volume of water in the vessel is decreasing when its height is 6ft. is
is full of water. If empties in such away that the height at the water in the vessel is decreasing at a constant rate of 1ft/min. Then the rate at which the volume of water in the vessel is decreasing when its height is 6ft. is
A conical vessel of height 10ft and semivertical angle  is full of water. If empties in such away that the height at the water in the vessel is decreasing at a constant rate of 1ft/min. Then the rate at which the volume of water in the vessel is decreasing when its height is 6ft. is
is full of water. If empties in such away that the height at the water in the vessel is decreasing at a constant rate of 1ft/min. Then the rate at which the volume of water in the vessel is decreasing when its height is 6ft. is
Maths-General
physics
If the gravitational force between two objects were proportional to  (and not as
(and not as  )where R is separation between them, then a particle in circular orbit under such a force would have, its orbital speed v proportional to
)where R is separation between them, then a particle in circular orbit under such a force would have, its orbital speed v proportional to
If the gravitational force between two objects were proportional to  (and not as
(and not as  )where R is separation between them, then a particle in circular orbit under such a force would have, its orbital speed v proportional to
)where R is separation between them, then a particle in circular orbit under such a force would have, its orbital speed v proportional to
physicsGeneral
Maths-
The surface area of a sphere increases at the rate of 1 sq. ft per second, then the rate of increase of volume when the radius is  is
is
The surface area of a sphere increases at the rate of 1 sq. ft per second, then the rate of increase of volume when the radius is  is
is
Maths-General
maths-
If  , then
, then  is equal to
is equal to
If  , then
, then  is equal to
is equal to
maths-General
chemistry-
Which of the following arrangements does not represent the correct order of the property stated against it?
Which of the following arrangements does not represent the correct order of the property stated against it?
chemistry-General
chemistry-
Magnetic moment of Cr (Z = 24), Mn+ (Z = 25) and Fe2+ (Z = 26) are a,b,c. They are in the order:
Magnetic moment of Cr (Z = 24), Mn+ (Z = 25) and Fe2+ (Z = 26) are a,b,c. They are in the order:
chemistry-General
physics
A geo-stationary satellite is orbiting the earth of a height of above the surface of earth, R. being the radius of earth. The time period of another satellite at a height of 2.5R from the surface fo earth is hr
A geo-stationary satellite is orbiting the earth of a height of above the surface of earth, R. being the radius of earth. The time period of another satellite at a height of 2.5R from the surface fo earth is hr
physicsGeneral



