Maths-
General
Easy
Question
If nCr denotes the number of combinations of n things taken r at a time, then the expression nCr+1 + nCr –1 + 2 × nCr equals-
- n + 1Cr +1
- n+2Cr
- n+2Cr+1
- n+1Cr

By choosing some items from a set and creating subsets, permutation and combination are two approaches to represent a group of objects. It outlines the numerous configurations for a particular set of data. Permutations are the selection of data or objects from a set, whereas combinations are the order in which they are represented. Here we have given nCr denotes the number of combinations of n things taken r at a time, we have to find the expression nCr+1 + nCr –1 + 2 × nCr.
The correct answer is: n+2Cr+1
A permutation is the non-replaceable selection of r items from a set of n items in which the order is important.

A combination is created by selecting r items from a group of n items without replacing them and without regard to their order.

Here we have given: nCr denotes the number of combinations of n things taken r at a time, so

The different ways in which items from a set may be chosen, usually without replacement, to construct subsets, are called permutations and combinations. When the order of the selection is a consideration, this selection of subsets is referred to as a permutation; when it is not, it is referred to as a combination. So the final answer is .
Related Questions to study
maths-
The number of ways is which an examiner can assign 30 marks to 8 questions, giving not less than 2 marks to any question is -
The number of ways is which an examiner can assign 30 marks to 8 questions, giving not less than 2 marks to any question is -
maths-General
physics-
An intense stream of water of cross-sectional area  strikes a wall at an angle
strikes a wall at an angle  with the normal to the wall and returns back elastically. If the density of water is
with the normal to the wall and returns back elastically. If the density of water is  and its velocity is
and its velocity is  ,then the force exerted in the wall will be
,then the force exerted in the wall will be

An intense stream of water of cross-sectional area  strikes a wall at an angle
strikes a wall at an angle  with the normal to the wall and returns back elastically. If the density of water is
with the normal to the wall and returns back elastically. If the density of water is  and its velocity is
and its velocity is  ,then the force exerted in the wall will be
,then the force exerted in the wall will be

physics-General
physics-
The force required to stretch a spring varies with the distance as shown in the figure. If the experiment is performed with above spring of half length, the line  will
will

The force required to stretch a spring varies with the distance as shown in the figure. If the experiment is performed with above spring of half length, the line  will
will

physics-General
physics-
Two small particles of equal masses start moving in opposite directions from a point  in a horizontal circular orbit. Their tangential velocities are
in a horizontal circular orbit. Their tangential velocities are  and
and  , respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at
, respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at  , these two particles will again reach the point
, these two particles will again reach the point 

Two small particles of equal masses start moving in opposite directions from a point  in a horizontal circular orbit. Their tangential velocities are
in a horizontal circular orbit. Their tangential velocities are  and
and  , respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at
, respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at  , these two particles will again reach the point
, these two particles will again reach the point 

physics-General
maths-
In a model, it is shown that an arch of abridge is semi-elliptical with major axis horizontal. If the length of the base is 9 m and the highest part of the bridge is 3 m from the horizontal, the best approximation of the height of the arch, 2 m from the centre of the base is
In a model, it is shown that an arch of abridge is semi-elliptical with major axis horizontal. If the length of the base is 9 m and the highest part of the bridge is 3 m from the horizontal, the best approximation of the height of the arch, 2 m from the centre of the base is
maths-General
maths-
The number of non-negative integral solutions of x + y + z n, where n N is -
The number of non-negative integral solutions of x + y + z n, where n N is -
maths-General
maths-
Between two junction stations A and B there are 12 intermediate stations. The number of ways in which a train can be made to stop at 4 of these stations so that no two of these halting stations are consecutive is -
Between two junction stations A and B there are 12 intermediate stations. The number of ways in which a train can be made to stop at 4 of these stations so that no two of these halting stations are consecutive is -
maths-General
maths-
If n objects are arranged in a row, then the number of ways of selecting three of these objects so that no two of them are next to each other is -
If n objects are arranged in a row, then the number of ways of selecting three of these objects so that no two of them are next to each other is -
maths-General
Maths-
The number of numbers between 1 and 1010 which contain the digit 1 is -
The number of numbers between 1 and 1010 which contain the digit 1 is -
Maths-General
Maths-
The number of rectangles in the adjoining figure is –

The number of rectangles in the adjoining figure is –

Maths-General
chemistry-
Assertion :this equilibrium favours backward direction.
Reason :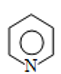 is stronger base than
is stronger base than 
Assertion :this equilibrium favours backward direction.
Reason : is stronger base than
is stronger base than 
chemistry-General
Physics-
A 0.098 kg block slides down a frictionless track as shown. The vertical component of the velocity of block at  is
is
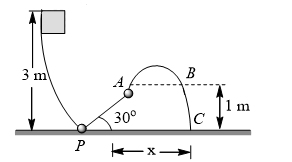
A 0.098 kg block slides down a frictionless track as shown. The vertical component of the velocity of block at  is
is

Physics-General
physics-
Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are  respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at
respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at  ,these two particles will again reach The point
,these two particles will again reach The point 

Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are  respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at
respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at  ,these two particles will again reach The point
,these two particles will again reach The point 

physics-General
physics-
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position  are
are  The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
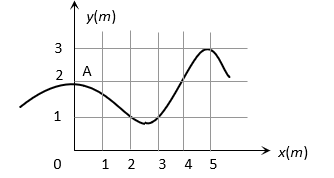
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position  are
are  The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are

physics-General
physics-
The potential energy of a particle varies with distance  as shown in the graph.
as shown in the graph.
The force acting on the particle is zero at

The potential energy of a particle varies with distance  as shown in the graph.
as shown in the graph.
The force acting on the particle is zero at

physics-General



