Maths-
General
Easy
Question
The number of numbers between 1 and 1010 which contain the digit 1 is -
- 1010 – 910 – 1
- 910
- 1010 – 810
- None of these.
The correct answer is: 1010 – 910 – 1
Related Questions to study
Maths-
The number of rectangles in the adjoining figure is –

The number of rectangles in the adjoining figure is –

Maths-General
chemistry-
Assertion :this equilibrium favours backward direction.
Reason : is stronger base than
is stronger base than 
Assertion :this equilibrium favours backward direction.
Reason : is stronger base than
is stronger base than 
chemistry-General
Physics-
A 0.098 kg block slides down a frictionless track as shown. The vertical component of the velocity of block at  is
is
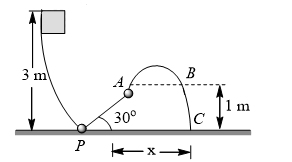
A 0.098 kg block slides down a frictionless track as shown. The vertical component of the velocity of block at  is
is

Physics-General
physics-
Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are  respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at
respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at  ,these two particles will again reach The point
,these two particles will again reach The point 

Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are  respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at
respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at  ,these two particles will again reach The point
,these two particles will again reach The point 

physics-General
physics-
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position  are
are  The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
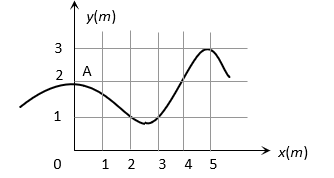
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position  are
are  The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are

physics-General
physics-
The potential energy of a particle varies with distance  as shown in the graph.
as shown in the graph.
The force acting on the particle is zero at

The potential energy of a particle varies with distance  as shown in the graph.
as shown in the graph.
The force acting on the particle is zero at

physics-General
physics-
A  mass moves along
mass moves along  -axis. Its acceleration as a function of its position is shown in the figure. What is the total work done on the mass by the force as the mass moves from
-axis. Its acceleration as a function of its position is shown in the figure. What is the total work done on the mass by the force as the mass moves from  to
to 

A  mass moves along
mass moves along  -axis. Its acceleration as a function of its position is shown in the figure. What is the total work done on the mass by the force as the mass moves from
-axis. Its acceleration as a function of its position is shown in the figure. What is the total work done on the mass by the force as the mass moves from  to
to 

physics-General
physics-
A mass  slips along the wall of a semispherical surface of radius
slips along the wall of a semispherical surface of radius  . The velocity at the bottom of the surface is
. The velocity at the bottom of the surface is

A mass  slips along the wall of a semispherical surface of radius
slips along the wall of a semispherical surface of radius  . The velocity at the bottom of the surface is
. The velocity at the bottom of the surface is

physics-General
physics-
Three forces of magnitudes 6N, 6N and  N at a corner of a cube along three sides as shown in figure. Resultant of these forces is
N at a corner of a cube along three sides as shown in figure. Resultant of these forces is

Three forces of magnitudes 6N, 6N and  N at a corner of a cube along three sides as shown in figure. Resultant of these forces is
N at a corner of a cube along three sides as shown in figure. Resultant of these forces is

physics-General
physics-
A man standing on a hill top projects a stone horizontally with speed  as shown in figure. Taking the coordinate system as given in the figure. The coordinates of the point where the stone will hit the hill surface
as shown in figure. Taking the coordinate system as given in the figure. The coordinates of the point where the stone will hit the hill surface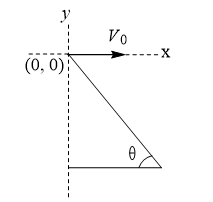
A man standing on a hill top projects a stone horizontally with speed  as shown in figure. Taking the coordinate system as given in the figure. The coordinates of the point where the stone will hit the hill surface
as shown in figure. Taking the coordinate system as given in the figure. The coordinates of the point where the stone will hit the hill surface
physics-General
physics-
A particle is acted upon by a force  which varies with position
which varies with position  as shown in the figure. If the particle at
as shown in the figure. If the particle at  has kinetic energy of 25 J, then the kinetic energy of the particle at
has kinetic energy of 25 J, then the kinetic energy of the particle at  is
is

A particle is acted upon by a force  which varies with position
which varies with position  as shown in the figure. If the particle at
as shown in the figure. If the particle at  has kinetic energy of 25 J, then the kinetic energy of the particle at
has kinetic energy of 25 J, then the kinetic energy of the particle at  is
is

physics-General
physics-
A bob of mass  accelerates uniformly from rest to
accelerates uniformly from rest to  in time
in time  . As a function of
. As a function of  , the instantaneous power delivered to the body is
, the instantaneous power delivered to the body is

A bob of mass  accelerates uniformly from rest to
accelerates uniformly from rest to  in time
in time  . As a function of
. As a function of  , the instantaneous power delivered to the body is
, the instantaneous power delivered to the body is

physics-General
physics-
An aeroplane is flying in a horizontal direction with a velocity  at a height of 1960 m. when it is vertically above the point
at a height of 1960 m. when it is vertically above the point  on the ground, a body is dropped from it. The body strikes the ground at point
on the ground, a body is dropped from it. The body strikes the ground at point  . Calculate the distance
. Calculate the distance 
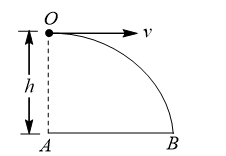
An aeroplane is flying in a horizontal direction with a velocity  at a height of 1960 m. when it is vertically above the point
at a height of 1960 m. when it is vertically above the point  on the ground, a body is dropped from it. The body strikes the ground at point
on the ground, a body is dropped from it. The body strikes the ground at point  . Calculate the distance
. Calculate the distance 

physics-General
Maths-
If the equation  represents an ellipse then
represents an ellipse then
If the equation  represents an ellipse then
represents an ellipse then
Maths-General
physics-
A particle of mass m moving with horizontal speed  as shown in figure. If
as shown in figure. If  than for one dimensional elastic collision, the speed of lighter particle after collision will be
than for one dimensional elastic collision, the speed of lighter particle after collision will be

A particle of mass m moving with horizontal speed  as shown in figure. If
as shown in figure. If  than for one dimensional elastic collision, the speed of lighter particle after collision will be
than for one dimensional elastic collision, the speed of lighter particle after collision will be

physics-General



