Maths-
General
Easy
Question
Statement I : Graph of y = tan x is symmetrical about origin
Statement II : Graph of  is symmetrical about y-axis
is symmetrical about y-axis
- If both (A) and (R) are true, and (R) is the correct explanation of (A) .
- If both (A) and (R) are true but (R) is not the correct explanation of (A) .
- If (A) is true but (R) is false.
- If (A) is false but (R) is true.
The correct answer is: If both (A) and (R) are true, and (R) is the correct explanation of (A) .
y = tan x is odd function so must be symmetrical about origin &  is decretive of y = tan x so it must be even imply symmetrical about y-axis or vice-versa
is decretive of y = tan x so it must be even imply symmetrical about y-axis or vice-versa
Related Questions to study
maths-
Statement-  If
If  Where
Where  is an identity function.
is an identity function.
Statement-  R defined by
R defined by  is an identity function.
is an identity function.
Statement-  If
If  Where
Where  is an identity function.
is an identity function.
Statement-  R defined by
R defined by  is an identity function.
is an identity function.
maths-General
Maths-
Assertion (A) : 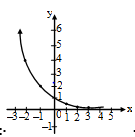 Graph of
Graph of 
Reason (R) : In the expression am/n, where a, m, n × J+, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.
Assertion (A) :  Graph of
Graph of 
Reason (R) : In the expression am/n, where a, m, n × J+, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.
Maths-General
maths-
Assertion: The period of  is 1/2.
is 1/2.
Reason: The period of x – [x] is 1.
Assertion: The period of  is 1/2.
is 1/2.
Reason: The period of x – [x] is 1.
maths-General
Maths-
Assertion : Fundamental period of  .
.
Reason : If the period of f(x) is  and the period of g(x) is
and the period of g(x) is  , then the fundamental period of f(x) + g(x) is the L.C.M. of
, then the fundamental period of f(x) + g(x) is the L.C.M. of  and T
and T
Assertion : Fundamental period of  .
.
Reason : If the period of f(x) is  and the period of g(x) is
and the period of g(x) is  , then the fundamental period of f(x) + g(x) is the L.C.M. of
, then the fundamental period of f(x) + g(x) is the L.C.M. of  and T
and T
Maths-General
Maths-
Assertion: The function defined by  is invertible if and only if
is invertible if and only if  .
.
Reason: A function is invertible if and only if it is one-to-one and onto function.
Assertion: The function defined by  is invertible if and only if
is invertible if and only if  .
.
Reason: A function is invertible if and only if it is one-to-one and onto function.
Maths-General
Maths-
Assertion :  can never become positive.
can never become positive.
Reason : f(x) = sgn x is always a positive function.
Assertion :  can never become positive.
can never become positive.
Reason : f(x) = sgn x is always a positive function.
Maths-General
Maths-
If f (x) = 
If f (x) = 
Maths-General
Maths-
The value of the integral  dx is :
dx is :
The value of the integral  dx is :
dx is :
Maths-General
Maths-
Assertion : Let  be a function defined by f(x) =
be a function defined by f(x) =  . Then f is many-one function.
. Then f is many-one function.
Reason : If either  or
or  domain of f, then y = f(x) is one-one function.</span
domain of f, then y = f(x) is one-one function.</span
Assertion : Let  be a function defined by f(x) =
be a function defined by f(x) =  . Then f is many-one function.
. Then f is many-one function.
Reason : If either  or
or  domain of f, then y = f(x) is one-one function.</span
domain of f, then y = f(x) is one-one function.</span
Maths-General
Maths-
Assertion : Fundamental period of  .
.
Reason : If the period of f(x) is  and the period of g(x) is
and the period of g(x) is  , then the fundamental period of f(x) + g(x) is the L.C.M. of
, then the fundamental period of f(x) + g(x) is the L.C.M. of  and T
and T
Assertion : Fundamental period of  .
.
Reason : If the period of f(x) is  and the period of g(x) is
and the period of g(x) is  , then the fundamental period of f(x) + g(x) is the L.C.M. of
, then the fundamental period of f(x) + g(x) is the L.C.M. of  and T
and T
Maths-General
Maths-
Function f(x) = 2x + 1 is-
f(x) = 2x + 1 is-
Function f(x) = 2x + 1 is-
f(x) = 2x + 1 is-
Maths-General
maths-
If f(x) is an even function and  Exist for all 'X' then f'(1)+f'(-1) is-
Exist for all 'X' then f'(1)+f'(-1) is-
If f(x) is an even function and  Exist for all 'X' then f'(1)+f'(-1) is-
Exist for all 'X' then f'(1)+f'(-1) is-
maths-General
physics-
In two separate collisions, the coefficient of restitutions and are in the ratio 3:1.In the first collision the relative velocity of approach is twice the relative velocity of separation ,then the ratio between relative velocity of approach and the relative velocity of separation in the second collision is
In two separate collisions, the coefficient of restitutions and are in the ratio 3:1.In the first collision the relative velocity of approach is twice the relative velocity of separation ,then the ratio between relative velocity of approach and the relative velocity of separation in the second collision is
physics-General
Maths-
Suppose  for
for . If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals–
. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals–
Suppose  for
for . If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals–
. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals–
Maths-General
Maths-
A spotlight installed in the ground shines on a wall. A woman stands between the light and the wall casting a shadow on the wall. How are the rate at which she walks away from the light and rate at which her shadow grows related ?

A spotlight installed in the ground shines on a wall. A woman stands between the light and the wall casting a shadow on the wall. How are the rate at which she walks away from the light and rate at which her shadow grows related ?

Maths-General



