Maths-

General

Easy

Question

Tangents are drawn to the ellipse $fraction numerator x to the power of 2 end exponent over denominator 9 end fraction plus fraction numerator y to the power of 2 end exponent over denominator 5 end fraction equals 1$ at the ends of the latus rectum. The are of the quadrilateral so formed is

27
$\frac{13}{2}$
$\frac{15}{4}$
45

hint Hint:

The eccentricity of an ellipse is always less than 1. i.e. e < 1. The eccentricity of an ellipse can be taken as the ratio of its distance from the focus and the distance from the directrix.
Eccentricity of ellipse (e) = $square root of 1 minus b squared over a squared end root$
Here a is the length of the semi-major axis and b is the length of the semi-minor axis.

The correct answer is: 27

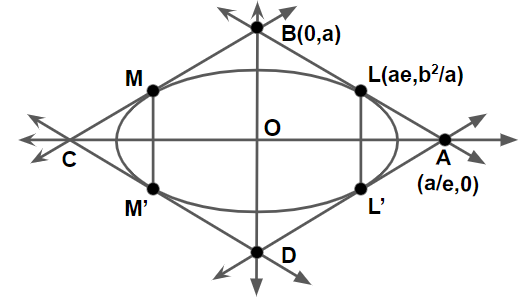
Let $L L^{'}$ and $M M^{'}$ are the latus rectum.
Eccentricity of ellipse (e) = $square root of 1 minus b squared over a squared end root$
Here a is the length of the semi-major axis and b is the length of the semi-minor axis.
$e space equals space square root of 1 space minus space b squared over a squared end root F r o m comma space x squared over 9 space plus space y squared over 5 space equals 1 b squared space equals space 5 space a n d space a squared space equals space 9 e space equals space square root of 1 space minus space 5 over 9 end root e space equals space 2 over 3$
The equation of tangent at $(x_{1}, y_{1})$ is $fraction numerator x x subscript 1 over denominator 9 end fraction space plus space fraction numerator y y subscript 1 over denominator 5 end fraction space equals space 1$
The tangent passes through point $b squared over a right parenthesis$
$S o comma space fraction numerator x left parenthesis a e right parenthesis over denominator 9 end fraction space plus space fraction numerator y left parenthesis begin display style b squared over a end style right parenthesis over denominator 5 end fraction space equals 1 space space space space space space rightwards double arrow e x space plus space y space equals space a space space space space space space rightwards double arrow fraction numerator x over denominator begin display style a over e end style end fraction plus space y over a space equals space 1$
$So, the tangent cuts the x-axis at point A(a/e,0) and y-axis at point B(0,a)$
$Area of quadrilateral ABCD = 4\timesarea of △OAB$
$4 space cross times 1 half cross times a over e cross times a$
$2 space cross times a squared over e$
$2 space space cross times space fraction numerator 9 over denominator begin display style 2 over 3 end style end fraction$
$Area of quadrilateral ABCD = 27sq. units$

A tangent to the ellipse x² + 4y² = 4 meets the ellipse x² + 2y² = 6 at P and Q. The angle between the tangents at P and Q of the ellipse x² + 2y² = 6 is

Maths-General

General

physics

Here are the graphs of x→ t of moving body. which of them is not suitable?

physicsGeneral

General

Maths-

A cubic polynomial f(x) = ax³ + bx² + cx + d has a graph which touches the x-axis at 2, has another x-intercept at –1 and has y-intercept at –2 as shown. The value of, a + b + c + d equals

If a function has a tangent at a point $x = a$ , then, it means, it is the critical point of that function and the derivative of the function is zero at that point.
Perform the calculations carefully, to avoid silly mistakes.
One should know how to read a graph to solve such questions.

A cubic polynomial f(x) = ax³ + bx² + cx + d has a graph which touches the x-axis at 2, has another x-intercept at –1 and has y-intercept at –2 as shown. The value of, a + b + c + d equals

Maths-General

General

Maths-

Consider f(x) = |1–x| 1 £ x £ 2 and g(x )= f(x) + b $sin invisible function application fraction numerator pi over denominator 2 end fraction x$ , 1 £ x £ 2 then which of the following is correct?

Maths-General

General

Maths-

The value of c in Lagrange’s theorem for the function f(x) = log sin x in the interval $open square brackets fraction numerator pi over denominator 6 end fraction comma fraction numerator 5 pi over denominator 6 end fraction close square brackets$ is -

Maths-General

General

physics

The relation between time and displacement of a moving particle is given by $t equals 2 a x squared$ where $alpha$ is a constant. The shape of the graph is $x not stretchy rightwards arrow y$ is....

physicsGeneral

General

Maths-

If P (q) and Q $open parentheses fraction numerator pi over denominator 2 end fraction plus theta close parentheses$ are two points on the ellipse $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ , then locus of the mid – point of PQ is

Maths-General

General

Maths-

If CP and CD are semi – conjugate diameters of an ellipse $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1 comma$ then CP² + CD² =

Maths-General

General

Maths-

The normals to the curve x = a ( $theta$ + sin $theta$ ), y = a (1 – cos $theta$ ) at the points $theta$ = (2n + 1) $pi$ , n $element of$ I are all -

Maths-General

General

Maths-

The normal to the curve x = 3 cos $theta$ – cos3 $theta$ , y = 3 sin $theta$ – sin3 $theta$ at the point $theta$ = $pi$ /4 passes through the point -

Maths-General

General

Maths-

The normal of the curve given by the equation x = a (sin $theta$ + cos $theta$ ), y = a (sin $theta$ – cos $theta$ ) at the point Q is -

Maths-General

General

Maths-

If the tangent at ‘t’ on the curve y = 8t3 –1, x = 4t2 + 3 meets the curve again at t¢ and is normal to the curve at that point, then value of t must be -

Maths-General

General

Maths-

The tangent at (t, t2 – t3) on the curve y = x2 – x3 meets the curve again at Q, then abscissa of Q must be -

Maths-General

General

Maths-

If $fraction numerator x over denominator a end fraction plus fraction numerator y over denominator b end fraction$ = 1 is a tangent to the curve x = 4t,y = $fraction numerator 4 over denominator t end fraction$ , t $element of$ R then -

Maths-General

General

Maths-

The line $fraction numerator x over denominator a end fraction$ + $fraction numerator y over denominator b end fraction$ = 1 touches the curve y = be-x/a at the point :

Maths-General

Have a query? Ask a Tutor!!

Can’t find what you’re looking for?

Tangents are drawn to the ellipse at the ends of the latus rectum. The are of the quadrilateral so formed is

27 45

The correct answer is: 27

Related Questions to study

A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. The angle between the tangents at P and Q of the ellipse x2 + 2y2 = 6 is

A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. The angle between the tangents at P and Q of the ellipse x2 + 2y2 = 6 is

Here are the graphs of x→ t of moving body. which of them is not suitable?

Here are the graphs of x→ t of moving body. which of them is not suitable?

A cubic polynomial f(x) = ax3 + bx2 + cx + d has a graph which touches the x-axis at 2, has another x-intercept at –1 and has y-intercept at –2 as shown. The value of, a + b + c + d equals

A cubic polynomial f(x) = ax3 + bx2 + cx + d has a graph which touches the x-axis at 2, has another x-intercept at –1 and has y-intercept at –2 as shown. The value of, a + b + c + d equals

Consider f(x) = |1–x| 1 £ x £ 2 and g(x )= f(x) + b , 1 £ x £ 2 then which of the following is correct?

Consider f(x) = |1–x| 1 £ x £ 2 and g(x )= f(x) + b , 1 £ x £ 2 then which of the following is correct?

The value of c in Lagrange’s theorem for the function f(x) = log sin x in the interval is -

The value of c in Lagrange’s theorem for the function f(x) = log sin x in the interval is -

The relation between time and displacement of a moving particle is given by where is a constant. The shape of the graph is is....

The relation between time and displacement of a moving particle is given by where is a constant. The shape of the graph is is....

If P (q) and Q are two points on the ellipse , then locus of the mid – point of PQ is

If P (q) and Q are two points on the ellipse , then locus of the mid – point of PQ is

If CP and CD are semi – conjugate diameters of an ellipse then CP2 + CD2 =

If CP and CD are semi – conjugate diameters of an ellipse then CP2 + CD2 =

The normals to the curve x = a ( + sin ), y = a (1 – cos ) at the points = (2n + 1) , n I are all -

The normals to the curve x = a ( + sin ), y = a (1 – cos ) at the points = (2n + 1) , n I are all -

The normal to the curve x = 3 cos – cos3, y = 3 sin – sin3 at the point = /4 passes through the point -

The normal to the curve x = 3 cos – cos3, y = 3 sin – sin3 at the point = /4 passes through the point -

The normal of the curve given by the equation x = a (sin + cos), y = a (sin – cos) at the point Q is -

The normal of the curve given by the equation x = a (sin + cos), y = a (sin – cos) at the point Q is -

If the tangent at ‘t’ on the curve y = 8t3 –1, x = 4t2 + 3 meets the curve again at t¢ and is normal to the curve at that point, then value of t must be -

If the tangent at ‘t’ on the curve y = 8t3 –1, x = 4t2 + 3 meets the curve again at t¢ and is normal to the curve at that point, then value of t must be -

The tangent at (t, t2 – t3) on the curve y = x2 – x3 meets the curve again at Q, then abscissa of Q must be -

The tangent at (t, t2 – t3) on the curve y = x2 – x3 meets the curve again at Q, then abscissa of Q must be -

If = 1 is a tangent to the curve x = 4t,y =, t R then -

If = 1 is a tangent to the curve x = 4t,y =, t R then -

The line + = 1 touches the curve y = be-x/a at the point :

The line + = 1 touches the curve y = be-x/a at the point :

With Turito Academy.

With Turito Foundation.

Get an Expert Advice From Turito.

Turito Academy

With Turito Academy.

Test Prep

With Turito Foundation.

Courses

Quick Links

Tangents are drawn to the ellipse $fraction numerator x to the power of 2 end exponent over denominator 9 end fraction plus fraction numerator y to the power of 2 end exponent over denominator 5 end fraction equals 1$ at the ends of the latus rectum. The are of the quadrilateral so formed is

27
$\frac{13}{2}$
$\frac{15}{4}$
45

A tangent to the ellipse x² + 4y² = 4 meets the ellipse x² + 2y² = 6 at P and Q. The angle between the tangents at P and Q of the ellipse x² + 2y² = 6 is

A tangent to the ellipse x² + 4y² = 4 meets the ellipse x² + 2y² = 6 at P and Q. The angle between the tangents at P and Q of the ellipse x² + 2y² = 6 is

A cubic polynomial f(x) = ax³ + bx² + cx + d has a graph which touches the x-axis at 2, has another x-intercept at –1 and has y-intercept at –2 as shown. The value of, a + b + c + d equals

A cubic polynomial f(x) = ax³ + bx² + cx + d has a graph which touches the x-axis at 2, has another x-intercept at –1 and has y-intercept at –2 as shown. The value of, a + b + c + d equals

Consider f(x) = |1–x| 1 £ x £ 2 and g(x )= f(x) + b $sin invisible function application fraction numerator pi over denominator 2 end fraction x$ , 1 £ x £ 2 then which of the following is correct?

Consider f(x) = |1–x| 1 £ x £ 2 and g(x )= f(x) + b $sin invisible function application fraction numerator pi over denominator 2 end fraction x$ , 1 £ x £ 2 then which of the following is correct?

The value of c in Lagrange’s theorem for the function f(x) = log sin x in the interval $open square brackets fraction numerator pi over denominator 6 end fraction comma fraction numerator 5 pi over denominator 6 end fraction close square brackets$ is -

The value of c in Lagrange’s theorem for the function f(x) = log sin x in the interval $open square brackets fraction numerator pi over denominator 6 end fraction comma fraction numerator 5 pi over denominator 6 end fraction close square brackets$ is -

The relation between time and displacement of a moving particle is given by $t equals 2 a x squared$ where $alpha$ is a constant. The shape of the graph is $x not stretchy rightwards arrow y$ is....

The relation between time and displacement of a moving particle is given by $t equals 2 a x squared$ where $alpha$ is a constant. The shape of the graph is $x not stretchy rightwards arrow y$ is....

The normals to the curve x = a ( $theta$ + sin $theta$ ), y = a (1 – cos $theta$ ) at the points $theta$ = (2n + 1) $pi$ , n $element of$ I are all -

The normals to the curve x = a ( $theta$ + sin $theta$ ), y = a (1 – cos $theta$ ) at the points $theta$ = (2n + 1) $pi$ , n $element of$ I are all -

The normal to the curve x = 3 cos $theta$ – cos3 $theta$ , y = 3 sin $theta$ – sin3 $theta$ at the point $theta$ = $pi$ /4 passes through the point -

The normal to the curve x = 3 cos $theta$ – cos3 $theta$ , y = 3 sin $theta$ – sin3 $theta$ at the point $theta$ = $pi$ /4 passes through the point -

The normal of the curve given by the equation x = a (sin $theta$ + cos $theta$ ), y = a (sin $theta$ – cos $theta$ ) at the point Q is -

The normal of the curve given by the equation x = a (sin $theta$ + cos $theta$ ), y = a (sin $theta$ – cos $theta$ ) at the point Q is -

If $fraction numerator x over denominator a end fraction plus fraction numerator y over denominator b end fraction$ = 1 is a tangent to the curve x = 4t,y = $fraction numerator 4 over denominator t end fraction$ , t $element of$ R then -

If $fraction numerator x over denominator a end fraction plus fraction numerator y over denominator b end fraction$ = 1 is a tangent to the curve x = 4t,y = $fraction numerator 4 over denominator t end fraction$ , t $element of$ R then -

The line $fraction numerator x over denominator a end fraction$ + $fraction numerator y over denominator b end fraction$ = 1 touches the curve y = be-x/a at the point :

The line $fraction numerator x over denominator a end fraction$ + $fraction numerator y over denominator b end fraction$ = 1 touches the curve y = be-x/a at the point :