Maths-
General
Easy
Question
The area bounded by y=cos x, y=x+1 and y=0 in the second quadrant is
- 3/2 sq units
- 2 sq units
- 1 sq unit
- 1/2 sq units
The correct answer is: 1/2 sq units
Related Questions to study
physics-
A 
joint is formed by two identical rods 
and 
each of mass 
and length 
in the 
plane as shown. Its moment of inertia about axis coinciding with is
A joint is formed by two identical rods and each of mass and length in the plane as shown. Its moment of inertia about axis coinciding with is
physics-General
Maths-
The area bounded by the parabola
=4ay, x-axis and the straight-line y=2a is
The area bounded by the parabola=4ay, x-axis and the straight-line y=2a is
Maths-General
physics-
Four balls each of radius 10 cm and mass 1 kg, 2kg, 3 kg and 4 kg are attached to the periphery of massless plate of radius 1 m. What is moment of inertia of the system about the centre of plate?
Four balls each of radius 10 cm and mass 1 kg, 2kg, 3 kg and 4 kg are attached to the periphery of massless plate of radius 1 m. What is moment of inertia of the system about the centre of plate?
physics-General
physics-
For the given uniform square lamina 
, whose centre is 
For the given uniform square lamina , whose centre is
physics-General
chemistry-
Which is correct about the change given below
Which is correct about the change given below
chemistry-General
chemistry-
Identify Z in the reaction 
Identify Z in the reaction
chemistry-General
chemistry-
X and Y are respectively
X and Y are respectively
chemistry-General
chemistry-
The product A is
The product A is
chemistry-General
chemistry-
Y is
Y is
chemistry-General
chemistry-
For which of the following molecule significant m ¹ 0
I)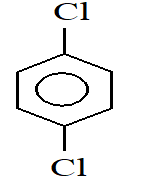 
II)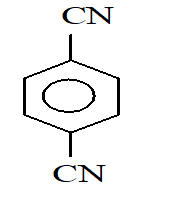 
III)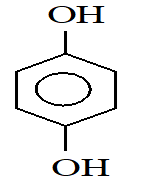 
IV)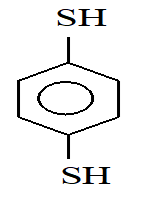 
For which of the following molecule significant m ¹ 0
I)
II)
III)
IV)
chemistry-General
chemistry-
Which one of the following will be the major product when
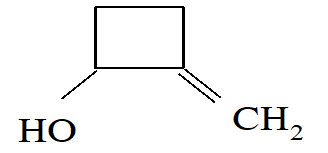
Is treated with dilute H2SO4 in the presence of HgSO4
Which one of the following will be the major product when
Is treated with dilute H2SO4 in the presence of HgSO4
chemistry-General
chemistry-
The appropriate reagent (s) for the transformation
is / are
The appropriate reagent (s) for the transformation
is / are
chemistry-General
chemistry-
The most suitable reagent of r the conversion of RCH2OH → RCHO is
The most suitable reagent of r the conversion of RCH2OH → RCHO is
chemistry-General
chemistry-
Which alkali metal floats over cold water without any reaction?
Which alkali metal floats over cold water without any reaction?
chemistry-General
physics-
The radius of germanium (
) nuclide is measured to be twice the radius of 
. The number of nucleons in Ge are
The radius of germanium () nuclide is measured to be twice the radius of . The number of nucleons in Ge are
physics-General
