Physics-
General
Easy
Question
A particle starts from rest at 
and undergoes an acceleration a in 
with time 
in seconds which is as shown
Which one of the following plot represents velocity 
in 
versus time in seconds
The correct answer is:
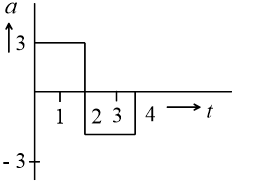
Takingthe motion from 
to 
Taking the motion from to 
Related Questions to study
Maths-
Period of 
is
Period of is
Maths-General
physics-
Two inclined planes are located as shown in figure. A particle is projected from the foot of one frictionless plane along its line with a velocity just sufficient to carry it to top after which the particle slides down the other frictionless inclined plane. The total time it will take to reach the point 
is
Two inclined planes are located as shown in figure. A particle is projected from the foot of one frictionless plane along its line with a velocity just sufficient to carry it to top after which the particle slides down the other frictionless inclined plane. The total time it will take to reach the point is
physics-General
physics-
characteristic of a copper wire of length 
and area of cross-section 
is shown in figure. The slope of the curve becomes
characteristic of a copper wire of length and area of cross-section is shown in figure. The slope of the curve becomes
physics-General
physics-
Four concurrent coplanar forces in newton are acting at a point and keep it in equilibrium figure. Then values of 
and 
are
Four concurrent coplanar forces in newton are acting at a point and keep it in equilibrium figure. Then values of and are
physics-General
physics-
The effective capacitance between points 
and 
shown in figure. Assuming 
F and that outer capacitors are all 
F is
The effective capacitance between points and shown in figure. Assuming F and that outer capacitors are all F is
physics-General
physics-
The four capacitors, each of 25 
F are connected as shown in figure. The DC voltmeter reads 200 V. the change on each plate of capacitor is
The four capacitors, each of 25 F are connected as shown in figure. The DC voltmeter reads 200 V. the change on each plate of capacitor is
physics-General
physics-
For the circuit shown in figure the charge on 4F capacitor is
For the circuit shown in figure the charge on 4F capacitor is
physics-General
physics-
The variation of electric potential with distance from a fixed point is shown in figure. What is the value of electric field at 
=2 m.
The variation of electric potential with distance from a fixed point is shown in figure. What is the value of electric field at =2 m.
physics-General
Maths-
The integrating factor of the differential equation 
is given by
The integrating factor of the differential equation is given by
Maths-General
physics-
As shown in figure, if the point is earthed and the point is given a potential of 2000 V, then the potential at point 
will be
As shown in figure, if the point is earthed and the point is given a potential of 2000 V, then the potential at point will be
physics-General
physics-
The equivalent capacitance between points 
for the combination of capacitors shown in figure, where all capacitances are in microfarad is
The equivalent capacitance between points for the combination of capacitors shown in figure, where all capacitances are in microfarad is
physics-General
physics-
The effective capacitance between points 
is
The effective capacitance between points is
physics-General
physics-
A gang capacitor is formed by interlocking a number of plates as shown in figure. The distance between the consecutive plates is 0.885 cm and the overlapping area of the plates is 
The capacity of the unit is
A gang capacitor is formed by interlocking a number of plates as shown in figure. The distance between the consecutive plates is 0.885 cm and the overlapping area of the plates is The capacity of the unit is
physics-General
physics-
A parallel plate capacitor with air as the dielectric has capacitance 
A slab of dielectric constant 
and having the same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be
A parallel plate capacitor with air as the dielectric has capacitance A slab of dielectric constant and having the same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be
physics-General
physics-
Four capacitors are connected in a circuit as shown in the following figure. Calculate the effective capacitance between the points .
Four capacitors are connected in a circuit as shown in the following figure. Calculate the effective capacitance between the points .
physics-General
