Physics-
General
Easy
Question
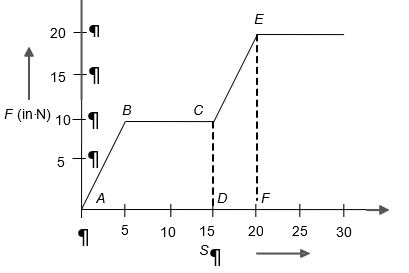
The work done by force acting on a body is as shown in the graph. The total work done in covering an initial distance of 20 m is
- 225 J
- 200 J
- 400 J
- 175 J
The correct answer is: 200 J
Work done 
ABCD +Area CEFD
Related Questions to study
physics-
Two rectangular blocks 
and 
of masses 2kg and 3 kg respectively are connected by spring of spring constant 10.8 
and are placed on a frictionless horizontal surface. The block was given an initial velocity of 0.15 
in the direction shown in the figure. The maximum compression of the spring during the motion is
Two rectangular blocks and of masses 2kg and 3 kg respectively are connected by spring of spring constant 10.8 and are placed on a frictionless horizontal surface. The block was given an initial velocity of 0.15 in the direction shown in the figure. The maximum compression of the spring during the motion is
physics-General
physics-
Six identical balls are linked in a straight groove made on a horizontal frictionless surface as shown. Two similar balls each moving with a velocity 
collide elastically with the row of 6 balls from left. What will happen
Six identical balls are linked in a straight groove made on a horizontal frictionless surface as shown. Two similar balls each moving with a velocity collide elastically with the row of 6 balls from left. What will happen
physics-General
physics-
A force 
acting on an object varies with distance 
as shown here. The force is in 
and in 
. The work done by the force in moving the object from 
to 
is
A force acting on an object varies with distance as shown here. The force is in and in . The work done by the force in moving the object from to is
physics-General
physics-
What is the velocity of the bob of a simple pendulum at its mean position, if it is able to rise to vertical height of 
(Take 
)
What is the velocity of the bob of a simple pendulum at its mean position, if it is able to rise to vertical height of (Take )
physics-General
physics-
The block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant k and compresses it by length L. The maximum momentum of the block after collides is
The block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant k and compresses it by length L. The maximum momentum of the block after collides is
physics-General
physics
The area covered by the curve of V-t graph and time axis is equal to magnitude of
The area covered by the curve of V-t graph and time axis is equal to magnitude of
physicsGeneral
physics-
In a children’s park, there is a slide which has a total length of 10 m and a height of 8.0 m. A vertical ladder is provided to reach the top. A boy weighing 200 N climbs up the ladder to the top of the slide and slides down to the ground. The average friction offered by the slide is three-tenth of his weight. The work done by the slide on the boy as he comes down is
In a children’s park, there is a slide which has a total length of 10 m and a height of 8.0 m. A vertical ladder is provided to reach the top. A boy weighing 200 N climbs up the ladder to the top of the slide and slides down to the ground. The average friction offered by the slide is three-tenth of his weight. The work done by the slide on the boy as he comes down is
physics-General
physics-
A mass ‘m’ moves with a velocity 'v’ and collides in elastically with another identical mass. After collision the Ist mass moves with velocity 
in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision
A mass ‘m’ moves with a velocity 'v’ and collides in elastically with another identical mass. After collision the Ist mass moves with velocity in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision
physics-General
physics-
A toy car of mass 5 kg moves up a ramp under the influence of force plotted against displacement . The maximum height attained is given by
A toy car of mass 5 kg moves up a ramp under the influence of force plotted against displacement . The maximum height attained is given by
physics-General
physics
In uniformly accelerated motion the slope of velocity - time graph gives ....
In uniformly accelerated motion the slope of velocity - time graph gives ....
physicsGeneral
physics
The graph of displacement (x) 
time (t) for an object is given in the figure. In which part of the graph the acceleration of the particle is positive ?
The graph of displacement (x) time (t) for an object is given in the figure. In which part of the graph the acceleration of the particle is positive ?
physicsGeneral
physics
In the above figure acceleration (a) time (t) graph is given. Hence 
In the above figure acceleration (a) time (t) graph is given. Hence
physicsGeneral
physics-
A block of mass 2kg is free to move along the x- axis. It is at rest and from t=0 onwards it is subjected to a time-dependent force 
in the x- direction. The force varies with t as shown in the figure. The kinetic energy of the block after 4.5 seconds is
A block of mass 2kg is free to move along the x- axis. It is at rest and from t=0 onwards it is subjected to a time-dependent force in the x- direction. The force varies with t as shown in the figure. The kinetic energy of the block after 4.5 seconds is
physics-General
physics-
The resultant of two forces, one double the other in magnitude, is perpendicular to the smaller of the two forces. The angle between the two forces is -
The resultant of two forces, one double the other in magnitude, is perpendicular to the smaller of the two forces. The angle between the two forces is -
physics-General
physics
Here is a velocity - time graph of a motorbike moving in one direction. Calculate the distance covered by it in last two seconds.
Here is a velocity - time graph of a motorbike moving in one direction. Calculate the distance covered by it in last two seconds.
physicsGeneral
