Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

What is the equivalent resistance between $A blank a n d blank B$ in the given circuit?

$4 Ω$
$2 Ω$
$\frac{8}{3} Ω$
$\frac{3}{8} Ω$

The correct answer is: $fraction numerator 8 over denominator 3 end fraction capital omega$

$R subscript 1 end subscript$ and $R subscript 2 end subscript$ are in series
$therefore blank R subscript 12 end subscript equals R subscript 1 end subscript plus R subscript 2 end subscript equals 4 capital omega$

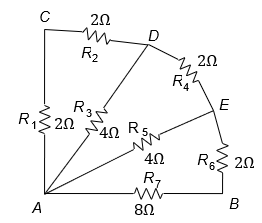
$R subscript 12 end subscript a n d R subscript 3 end subscript$ are in parallel
$R subscript 123 end subscript equals fraction numerator R subscript 3 end subscript cross times R subscript 12 end subscript over denominator R subscript 3 end subscript plus R subscript 12 end subscript end fraction$
$equals fraction numerator 4 cross times 4 over denominator 4 plus 4 end fraction$
$equals 2 capital omega$
$R subscript 123 end subscript$ and $R subscript 4 end subscript$ are in series
$therefore blank R subscript 1234 end subscript equals R subscript 123 end subscript plus R subscript 4 end subscript$
$equals 2 capital omega plus 2 capital omega$
$equals 4 capital omega$
$R subscript 1234 end subscript$ and $R subscript 5 end subscript$ are in parallel
$therefore R subscript 12345 end subscript equals 2 capital omega$
$R subscript 12345 end subscript$ and $R subscript 6 end subscript$ are in series
$2 capital omega plus 2 capital omega equals 4 capital omega$
$equals R subscript 123456 end subscript$
Now, $R subscript 123456 end subscript$ and $R subscript 7 end subscript$ are in parallel
$therefore R subscript c o m b end subscript equals fraction numerator 4 cross times 8 over denominator 4 plus 8 end fraction$
$equals fraction numerator 32 over denominator 12 end fraction equals fraction numerator 8 over denominator 3 end fraction capital omega$

Related Questions to study

The current in the 1 $capital omega$ resistor shown in the circuit is

The current in the 1 $capital omega$ resistor shown in the circuit is

physics-General

The current in the 1 $capital omega$ resistor shown in the circuit is

The current in the 1 $capital omega$ resistor shown in the circuit is

physics-General

The total current supplied to the given circuit by the battery is

The total current supplied to the given circuit by the battery is

physics-General

parallel

A current of 2A flows in an electric circuit as shown in figure. The potential difference $left parenthesis V subscript R end subscript minus V subscript S end subscript right parenthesis$ , in volts( $V subscript R end subscript minus V subscript S end subscript$ are potentials at R and S respectively) is

A current of 2A flows in an electric circuit as shown in figure. The potential difference $left parenthesis V subscript R end subscript minus V subscript S end subscript right parenthesis$ , in volts( $V subscript R end subscript minus V subscript S end subscript$ are potentials at R and S respectively) is

physics-General

A 3 V battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be

A 3 V battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be

physics-General

The equivalent resistance between the points A and B will be (each resistance is
15 $capital omega$ )

The equivalent resistance between the points A and B will be (each resistance is
15 $capital omega$ )

physics-General

parallel

There resistances of 4 $blank capital omega$ each are connected as shown in figure. If the point D divides the resistance into two equal halves, the resistance between points A and D will be

There resistances of 4 $blank capital omega$ each are connected as shown in figure. If the point D divides the resistance into two equal halves, the resistance between points A and D will be

physics-General

A particle starts from rest at $t equals 0$ and moves in a straight line with an acceleration as shown below. The velocity of the particle at $t equals 3 s blank$ is

A particle starts from rest at $t equals 0$ and moves in a straight line with an acceleration as shown below. The velocity of the particle at $t equals 3 s blank$ is

physics-General

Period of $sin space open parentheses e to the power of text sont end text end exponent plus e to the power of text cur end text end exponent close parentheses$ is

Period of $sin space open parentheses e to the power of text sont end text end exponent plus e to the power of text cur end text end exponent close parentheses$ is

parallel

Period of $fraction numerator sin space left parenthesis x plus a right parenthesis over denominator cos space x end fraction$

Period of $fraction numerator sin space left parenthesis x plus a right parenthesis over denominator cos space x end fraction$

In a network as shown in the figure, the potential difference across the resistance 2R is (the cell has an emf of E volt and has no ingternal resistance)

In a network as shown in the figure, the potential difference across the resistance 2R is (the cell has an emf of E volt and has no ingternal resistance)

physics-General

In the adjoining figure the equivalent resistance between A and B is

In the adjoining figure the equivalent resistance between A and B is

physics-General

parallel

The charge on the capacitor of capacitance $C$ shown in the figure below will be

The charge on the capacitor of capacitance $C$ shown in the figure below will be

physics-General

Each resistance shown in figure is 2 $blank capital omega$ . The equivalent resistance between A and B is

Each resistance shown in figure is 2 $blank capital omega$ . The equivalent resistance between A and B is

physics-General

The equivalent resistance across A and B is

The equivalent resistance across A and B is

physics-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.