Maths-
The pole of the straight line 9x + y – 28 = 0 with respect to the circle 
is
Maths-General
- (–3, 1)
- (1, 3)
- (3, – 1)
- (3, 1)
Answer:The correct answer is: (3, – 1)
Book A Free Demo
+91 
Grade*
Select Grade
Related Questions to study
physics-
The distance between a point source of light and a screen which is 60 cm is increased to 180 cm. The intensity on the screen as compared with the original intensity will be
The distance between a point source of light and a screen which is 60 cm is increased to 180 cm. The intensity on the screen as compared with the original intensity will be
physics-General
physics-
Three rods of equal length 
are joined to form an equilateral triangle 
O is the mid point of 
Distance 
remains same for small change in temperature. Coefficient of linear expansion for 
and 
is same, 
but that for 
is 
Then
Neglecting
and 
Three rods of equal length are joined to form an equilateral triangle O is the mid point of Distance remains same for small change in temperature. Coefficient of linear expansion for and is same, but that for is Then
physics-General
Neglecting
and physics-
A point source causes photoelectric effect from a small metal plate Which of the following curves may represent the saturation photocurrent as a function of the distance between the source and the metal?
A point source causes photoelectric effect from a small metal plate Which of the following curves may represent the saturation photocurrent as a function of the distance between the source and the metal?
physics-General
physics-
One of the following figures respesents the variation of particle momentum with associated de Broglie wavelength
a)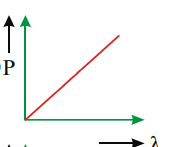 
b)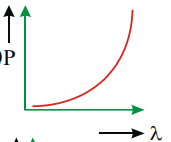 
c)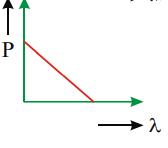 
One of the following figures respesents the variation of particle momentum with associated de Broglie wavelength
a)
b)
c)
physics-General
physics-
An electric lamp is fixed at the ceiling of a circular tunnel as shown is figure. What is the ratio the intensities of light at base A and a point B on the wall
and 
An electric lamp is fixed at the ceiling of a circular tunnel as shown is figure. What is the ratio the intensities of light at base A and a point B on the wall
physics-General
and maths-
If the line y = x + 3 meets the circle 
at A and B, then equation of the circle on AB as diameter is
If the line y = x + 3 meets the circle at A and B, then equation of the circle on AB as diameter is
maths-General
physics-
The figure shows a system of two concentric spheres of radii 
and 
and kept at temperatures 
and 
respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to
To measure the radial rate of heat flow, we have to go for integration technique as here the area of the surface through which heat will flow is not constant.
Let us consider an element (spherical shell) of thickness d
and radius as shown in figure. Let us first find the equivalent thermal resistance between inner and outer sphere.
Resistance of shell=
=
Rate of heat flow = H
=
=
Let us consider an element (spherical shell) of thickness d
and radius as shown in figure. Let us first find the equivalent thermal resistance between inner and outer sphere.Resistance of shell=
=
Rate of heat flow = H
=
=
The figure shows a system of two concentric spheres of radii and and kept at temperatures and respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to
physics-General
To measure the radial rate of heat flow, we have to go for integration technique as here the area of the surface through which heat will flow is not constant.
Let us consider an element (spherical shell) of thickness d and radius as shown in figure. Let us first find the equivalent thermal resistance between inner and outer sphere.
Resistance of shell=
=
Rate of heat flow = H
=
=
Let us consider an element (spherical shell) of thickness d
and radius as shown in figure. Let us first find the equivalent thermal resistance between inner and outer sphere.Resistance of shell=
=
Rate of heat flow = H
=
=
physics-
Two circular discs A and B with equal radii are blackened. They are heated to some temperature and are cooled under identical conditions. What inference do you draw from their cooling curves?
According to Newton’s law of cooling, rate of cooling is given by
Where c is specific heat of material.
or
rate of cooling varies inversely as specific heat. From the graph, for A rate of cooling is larger. Therefore, specific heat of A is smaller.
Where c is specific heat of material.
or
rate of cooling varies inversely as specific heat. From the graph, for A rate of cooling is larger. Therefore, specific heat of A is smaller.Two circular discs A and B with equal radii are blackened. They are heated to some temperature and are cooled under identical conditions. What inference do you draw from their cooling curves?
physics-General
According to Newton’s law of cooling, rate of cooling is given by
Where c is specific heat of material.
or
rate of cooling varies inversely as specific heat. From the graph, for A rate of cooling is larger. Therefore, specific heat of A is smaller.
Where c is specific heat of material.
or
rate of cooling varies inversely as specific heat. From the graph, for A rate of cooling is larger. Therefore, specific heat of A is smaller.physics-
Which of the curves in figure represents the relation between Celsius and Fahrenheit temperatures
Hence graph between 
and 
will be a straight line with positive slope and negative interceptWhich of the curves in figure represents the relation between Celsius and Fahrenheit temperatures
physics-General
Hence graph between and will be a straight line with positive slope and negative interceptmaths-
The area of circle centred at (1, 2) and passing through (4, 6) is
The area of circle centred at (1, 2) and passing through (4, 6) is
maths-General
physics-
Three rods of same dimensions are arranged as shown in figure. They have thermal conductivities 
and 
. The points 
and 
are maintained at different temperatures for the heat to flow at the same rate along 
and then which of the following options is correct
The given arrangement of rods can be redrawn as follows
It is given that
It is given that
Three rods of same dimensions are arranged as shown in figure. They have thermal conductivities and . The points and are maintained at different temperatures for the heat to flow at the same rate along and then which of the following options is correct
physics-General
The given arrangement of rods can be redrawn as follows
It is given that
It is given that
physics-
In the following diagram if 
then 
In the following diagram if then
physics-General
physics-
The maximum kinetic energy (Ek ) of emitted photoelectrons against frequency v of incident radiation is plotted as shown in fig The slope of the graph is equal to
The maximum kinetic energy (Ek ) of emitted photoelectrons against frequency v of incident radiation is plotted as shown in fig The slope of the graph is equal to
physics-General
physics-
Which of the substance 
or 
has the highest specific heat? The temperature 
time graph is shown
Substances having more specific heat take longer time to get heated to a higher temperature and longer time to get cooled.
If we draw a line parallel to the time axis then it cuts the given graphs at three different points. Corresponding points on the times axis shows that
If we draw a line parallel to the time axis then it cuts the given graphs at three different points. Corresponding points on the times axis shows that
Which of the substance or has the highest specific heat? The temperature time graph is shown
physics-General
Substances having more specific heat take longer time to get heated to a higher temperature and longer time to get cooled.
If we draw a line parallel to the time axis then it cuts the given graphs at three different points. Corresponding points on the times axis shows that
If we draw a line parallel to the time axis then it cuts the given graphs at three different points. Corresponding points on the times axis shows that
maths-
The equation of the circumcircle of the triangle formed by the lines 
and y=0 is
The equation of the circumcircle of the triangle formed by the lines and y=0 is
maths-General