Question
There are 12 balls numbered from 1 to 12 The number of ways in which they can be used to fill 8 places in a row is:

In the question we not only have to choose 8 balls from the 12 balls which are numbered but also we have to fill them in 8 places, So, we have to use the formula  .
.
The correct answer is: 
As we have to fill 8 places from 12 balls numbered 1 to 12.
So, the number of ways = 
Related Questions to study
If  then n is:
then n is:
If  then n is:
then n is:
If  then n is :
then n is :
If  then n is :
then n is :
If  then r is :
then r is :
If  then r is :
then r is :
In the figure given below, which blood vessel represents vena cava?

In the figure given below, which blood vessel represents vena cava?

Match the types of WBC listed under Column - I with the shape of nucleus given under Column - II and select the correct option from codes given below.
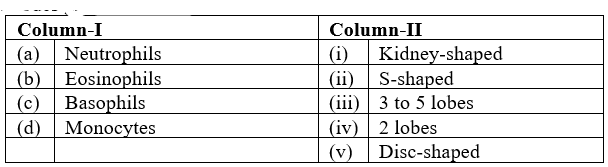
Match the types of WBC listed under Column - I with the shape of nucleus given under Column - II and select the correct option from codes given below.

The number of ways in which four letters can put in four addressed envelopes so that no letter goes into the envelope meant for it is :
The number of ways in which four letters can put in four addressed envelopes so that no letter goes into the envelope meant for it is :
In the given figure of the heart which of the labelled part (1, 2, 3, 4, 5) carries oxygenated blood?

In the given figure of the heart which of the labelled part (1, 2, 3, 4, 5) carries oxygenated blood?

The given figure shows an angiogram of the coronary blood vessel. Which one of the following statements correctly describes, what is being done?

The given figure shows an angiogram of the coronary blood vessel. Which one of the following statements correctly describes, what is being done?

There are 3 letters and 3 addressed envelopes corresponding to them. The number of ways in which the letters be placed in the envelopes so that no letter is in the right envelope is:
There are 3 letters and 3 addressed envelopes corresponding to them. The number of ways in which the letters be placed in the envelopes so that no letter is in the right envelope is:
Match Column - I with Column - II and select the correct option from the codes give below.

Match Column - I with Column - II and select the correct option from the codes give below.

The sum of all the numbers formed by taking all the digits from 3,4,5,6,7 is:
The sum of all the numbers formed by taking all the digits from 3,4,5,6,7 is:
The sum of all the numbers formed by taking all the digits from 2,3,4,5 is:
The sum of all the numbers formed by taking all the digits from 2,3,4,5 is:



