Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

If m and 2 s are the mean and variance of the random variable X, whose distribution is given by

$m = σ^{2} = 2$
$m = 1, σ^{2} = 2$
$m = σ^{2} = 1$
$m = 2, σ^{2} = 1$

The correct answer is: $m equals sigma to the power of 2 end exponent equals 1$

Related Questions to study

The distribution of a random variable X is given below

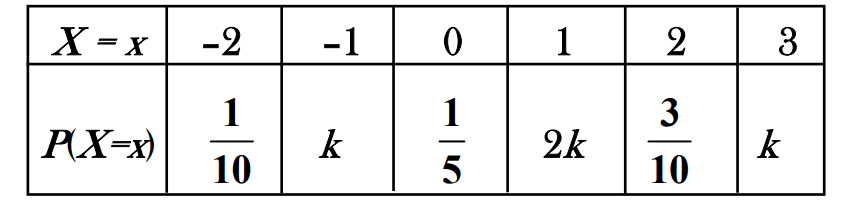
The value of k is

The distribution of a random variable X is given below

The value of k is

The number of different triangles formed by joining the points A, B, C, D, E, F and G as shown in the figure given below is

The number of different triangles formed by joining the points A, B, C, D, E, F and G as shown in the figure given below is

The number of ways that the letters of the word ”PERSON” can be placed in the squares of the adjoining figure so that no row remains empty

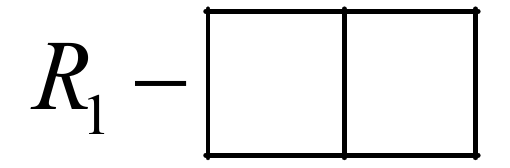
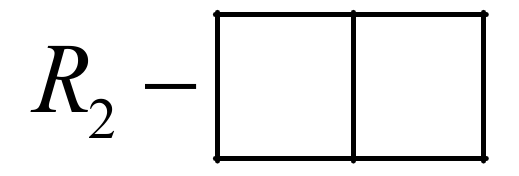
The number of ways that the letters of the word ”PERSON” can be placed in the squares of the adjoining figure so that no row remains empty

parallel

The value of $open vertical bar table row cell 1 to the power of 2 end exponent end cell cell 2 to the power of 2 end exponent end cell cell 3 to the power of 2 end exponent end cell row cell 2 to the power of 2 end exponent end cell cell 3 to the power of 2 end exponent end cell cell 4 to the power of 2 end exponent end cell row cell 3 to the power of 2 end exponent end cell cell 4 to the power of 2 end exponent end cell cell 5 to the power of 2 end exponent end cell end table close vertical bar$ is

The value of $open vertical bar table row cell 1 to the power of 2 end exponent end cell cell 2 to the power of 2 end exponent end cell cell 3 to the power of 2 end exponent end cell row cell 2 to the power of 2 end exponent end cell cell 3 to the power of 2 end exponent end cell cell 4 to the power of 2 end exponent end cell row cell 3 to the power of 2 end exponent end cell cell 4 to the power of 2 end exponent end cell cell 5 to the power of 2 end exponent end cell end table close vertical bar$ is

The determinant $open vertical bar table row a b cell a minus b end cell row b c cell b minus c end cell row 2 1 0 end table close vertical bar$ is equal to zero if $a comma b comma c$ are in

The determinant $open vertical bar table row a b cell a minus b end cell row b c cell b minus c end cell row 2 1 0 end table close vertical bar$ is equal to zero if $a comma b comma c$ are in

If $a not equal to 6 comma b comma c$ satisfy $open vertical bar table row a cell 2 b end cell cell 2 c end cell row 3 b c row 4 a b end table close vertical bar equals 0 comma$ then $a b c equals$

If $a not equal to 6 comma b comma c$ satisfy $open vertical bar table row a cell 2 b end cell cell 2 c end cell row 3 b c row 4 a b end table close vertical bar equals 0 comma$ then $a b c equals$

parallel

End product of the following sequence of reaction is :

End product of the following sequence of reaction is :

chemistry-General

Arrange in the increasing order of boiling points:
i)
ii)
iii)

iv)

Arrange in the increasing order of boiling points:
i)
ii)
iii)

iv)

chemistry-General

Number of rectangles in fig. shown which are not squares is

Number of rectangles in fig. shown which are not squares is

parallel

Digit at unit place of sum (1!)² +(2!)² +(3!)² ……… +(2008!)² is

Digit at unit place of sum (1!)² +(2!)² +(3!)² ……… +(2008!)² is

A person writes letters to 6 friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that at least 4 of them are in wrong envelopes ?

A person writes letters to 6 friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that at least 4 of them are in wrong envelopes ?

The total numbers of integral solutions for (x,y,z) such that xyz = 24 is

The total numbers of integral solutions for (x,y,z) such that xyz = 24 is

parallel

Number of ways in which 5 different toys can be distributed among 5 children if exactly one child do not get any toy

Number of ways in which 5 different toys can be distributed among 5 children if exactly one child do not get any toy

A seven digit number is in form of abcdefg (g, f, e, etc. are digits at units, tens, hundred place etc.) where a < b < c < d > e > f > g. The number of such numbers are

A seven digit number is in form of abcdefg (g, f, e, etc. are digits at units, tens, hundred place etc.) where a < b < c < d > e > f > g. The number of such numbers are

Number of ways in which 25 identical balls can be distributed among Ram, Shyam, Sunder and Ghanshyam such that atleast 1, 2, 3, and 4 balls are given to Ram, Shyam, Sunder and Ghanshyam respectively, is-

Number of ways in which 25 identical balls can be distributed among Ram, Shyam, Sunder and Ghanshyam such that atleast 1, 2, 3, and 4 balls are given to Ram, Shyam, Sunder and Ghanshyam respectively, is-

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.