Physics-
General
Easy
Question
A radar operates at wavelength 50.0 cm. If the beat freqency between the transmitted singal and the singal reflected from aircraft (
 ) is 1 kHz, then velocity of the aircraft will be
) is 1 kHz, then velocity of the aircraft will be
- 800 km/hr
- 900 km/hr
- 1000 km/hr
- 1032 km/hr
The correct answer is: 900 km/hr
when source is fixed and observer is moving towards it

when source is moving towards observer at rest




= 900 km/hr
Related Questions to study
Maths-
The locus of P such that PA2 + PB2 = 10 where A = (2, 0) and B = (4, 0) is
The locus of P such that PA2 + PB2 = 10 where A = (2, 0) and B = (4, 0) is
Maths-General
maths-
Let L = 0 is a tangent to ellipse  +
+  = 1 and S,
= 1 and S,  be its foci. If length of perpendicular from S on L = 0 is 2 then length of perpendicular from
be its foci. If length of perpendicular from S on L = 0 is 2 then length of perpendicular from  on L = 0 is
on L = 0 is
Let L = 0 is a tangent to ellipse  +
+  = 1 and S,
= 1 and S,  be its foci. If length of perpendicular from S on L = 0 is 2 then length of perpendicular from
be its foci. If length of perpendicular from S on L = 0 is 2 then length of perpendicular from  on L = 0 is
on L = 0 is
maths-General
maths-
The condition that the line  x + my = n may be a normal to the ellipse
x + my = n may be a normal to the ellipse  +
+  = 1 is
= 1 is
The condition that the line  x + my = n may be a normal to the ellipse
x + my = n may be a normal to the ellipse  +
+  = 1 is
= 1 is
maths-General
Physics-
Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity). Normal reaction (in N) acting on block A.
). (g is acceleration due to gravity). Normal reaction (in N) acting on block A.

Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity). Normal reaction (in N) acting on block A.
). (g is acceleration due to gravity). Normal reaction (in N) acting on block A.

Physics-General
physics-
Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity) Normal reaction (in N) acting on block B is
). (g is acceleration due to gravity) Normal reaction (in N) acting on block B is

Two blocks A and B of equal masses m kg each are connected by a light thread, which passes over a massless pulley as shown in the figure. Both the blocks lie on wedge of mass m kg. Assume friction to be absent everywhere and both the blocks to be always in contact with the wedge. The wedge lying over smooth horizontal surface is pulled towards right with constant acceleration a ( ). (g is acceleration due to gravity) Normal reaction (in N) acting on block B is
). (g is acceleration due to gravity) Normal reaction (in N) acting on block B is

physics-General
physics-
A light inextensible string connects a block of mass m and top of wedge of mass M. The string is parallel to inclined surface and the inclined surface makes an angle  with horizontal as shown in the figure. All surfaces are smooth. Now a constant horizontal force of minimum magnitude F is applied to wedge towards right such that the normal reaction on block exerted by wedge just becomes zero. The magnitude of acceleration of wedge is
with horizontal as shown in the figure. All surfaces are smooth. Now a constant horizontal force of minimum magnitude F is applied to wedge towards right such that the normal reaction on block exerted by wedge just becomes zero. The magnitude of acceleration of wedge is

A light inextensible string connects a block of mass m and top of wedge of mass M. The string is parallel to inclined surface and the inclined surface makes an angle  with horizontal as shown in the figure. All surfaces are smooth. Now a constant horizontal force of minimum magnitude F is applied to wedge towards right such that the normal reaction on block exerted by wedge just becomes zero. The magnitude of acceleration of wedge is
with horizontal as shown in the figure. All surfaces are smooth. Now a constant horizontal force of minimum magnitude F is applied to wedge towards right such that the normal reaction on block exerted by wedge just becomes zero. The magnitude of acceleration of wedge is

physics-General
maths-
The vector  which is perpendicular to (2,-3,1) and (1,-2,3) and which satisfies the condition
which is perpendicular to (2,-3,1) and (1,-2,3) and which satisfies the condition 
The vector  which is perpendicular to (2,-3,1) and (1,-2,3) and which satisfies the condition
which is perpendicular to (2,-3,1) and (1,-2,3) and which satisfies the condition 
maths-General
Maths-
Let f : R → R be a differentiable function satisfying f (x) = f (x – y) f (y) " x, y Î R and f ¢ (0) = a, f ¢ (2) = b then f ¢ (-2) is
Let f : R → R be a differentiable function satisfying f (x) = f (x – y) f (y) " x, y Î R and f ¢ (0) = a, f ¢ (2) = b then f ¢ (-2) is
Maths-General
physics-
Four identical metal butterflies are hanging from a light string of length  at equally placed points as shown in the figure . The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle
at equally placed points as shown in the figure . The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle  and
and  is given by
is given by

Four identical metal butterflies are hanging from a light string of length  at equally placed points as shown in the figure . The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle
at equally placed points as shown in the figure . The ends of the string are attached to a horizontal fixed support. The middle section of the string is horizontal. The relation between the angle  and
and  is given by
is given by

physics-General
physics-
Initially the spring is undeformed. Now the force 'F' is applied to 'B' as shown in the figure . When the displacement of 'B' w.r.t 'A' is 'x' towards right in some time then the relative acceleration of 'B' w.r.t. 'A' at that moment is:

Initially the spring is undeformed. Now the force 'F' is applied to 'B' as shown in the figure . When the displacement of 'B' w.r.t 'A' is 'x' towards right in some time then the relative acceleration of 'B' w.r.t. 'A' at that moment is:

physics-General
physics-
Mass m shown in the figure is in equilibrium. If it is displaced further by x and released find its acceleration just after it is released. Take pulleys to be light & smooth and strings light.

Mass m shown in the figure is in equilibrium. If it is displaced further by x and released find its acceleration just after it is released. Take pulleys to be light & smooth and strings light.

physics-General
physics-
In the figure shown, the pulleys and strings are massless. The acceleration of the block of mass 4m just after the system is released from rest is 

In the figure shown, the pulleys and strings are massless. The acceleration of the block of mass 4m just after the system is released from rest is 

physics-General
maths-
If S and  are two foci of an ellipse
are two foci of an ellipse  +
+ = 1
= 1  and P
and P  a point on it, then SP +
a point on it, then SP +  P is equal to-
P is equal to-
If S and  are two foci of an ellipse
are two foci of an ellipse  +
+ = 1
= 1  and P
and P  a point on it, then SP +
a point on it, then SP +  P is equal to-
P is equal to-
maths-General
physics-
A cylinder rests in a supporting carriage as shown. The side AB of carriage makes an angle  with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration 'a'. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be
with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration 'a'. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be  respectively. Neglect friction everywhere. Then as the magnitude of acceleration 'a ' of the carriage is increased, pick up the correct statement:
respectively. Neglect friction everywhere. Then as the magnitude of acceleration 'a ' of the carriage is increased, pick up the correct statement:

A cylinder rests in a supporting carriage as shown. The side AB of carriage makes an angle  with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration 'a'. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be
with the horizontal and side BC is vertical. The carriage lies on a fixed horizontal surface and is being pulled towards left with an horizontal acceleration 'a'. The magnitude of normal reactions exerted by sides AB and BC of carriage on the cylinder be  respectively. Neglect friction everywhere. Then as the magnitude of acceleration 'a ' of the carriage is increased, pick up the correct statement:
respectively. Neglect friction everywhere. Then as the magnitude of acceleration 'a ' of the carriage is increased, pick up the correct statement:

physics-General
physics-
In the figure shown, a person wants to raise a block lying on the ground to a height h. In both the cases if time required is same then in which case he has to exert more force. Assume pulleys and strings light.
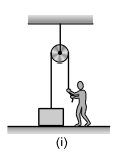

In the figure shown, a person wants to raise a block lying on the ground to a height h. In both the cases if time required is same then in which case he has to exert more force. Assume pulleys and strings light.


physics-General



