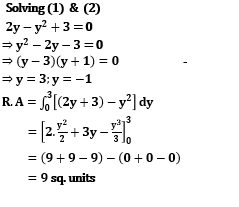Maths-
General
Easy
Question
The area (in square units)bounded by the curves y= a x is, and lying in the first quadrant is
a x is, and lying in the first quadrant is

- 36
- 18
- 27/4
- 9
The correct answer is: 9
Related Questions to study
maths-
The area under the curve y= and above x-axis is:
and above x-axis is:

The area under the curve y= and above x-axis is:
and above x-axis is:

maths-General
maths-
The area of the region (in sq. units), in the first quadrant, bounded by the parabola y= and the lines x=0,y=1 and y=4 is:
and the lines x=0,y=1 and y=4 is:

The area of the region (in sq. units), in the first quadrant, bounded by the parabola y= and the lines x=0,y=1 and y=4 is:
and the lines x=0,y=1 and y=4 is:

maths-General
maths-
The area bounded by the curve y=ln (x) and the lines y=0, y=ln(3) and x=0 is equal to:

The area bounded by the curve y=ln (x) and the lines y=0, y=ln(3) and x=0 is equal to:

maths-General
maths-
Let A= The area (in square units) of the region A is:
The area (in square units) of the region A is:

Let A= The area (in square units) of the region A is:
The area (in square units) of the region A is:

maths-General
maths-
The area (in sq units) of the region bounded by the curves and
and  is
is

The area (in sq units) of the region bounded by the curves and
and  is
is

maths-General
maths-
The area between the parabolas 4a(x+a) and
4a(x+a) and
 =-4a(x-a)in sQ units….
=-4a(x-a)in sQ units….

The area between the parabolas 4a(x+a) and
4a(x+a) and
 =-4a(x-a)in sQ units….
=-4a(x-a)in sQ units….

maths-General
maths-
The area of the region between the curve 4 and x = 0; x =1 is….
4 and x = 0; x =1 is….

The area of the region between the curve 4 and x = 0; x =1 is….
4 and x = 0; x =1 is….

maths-General
maths-
The area of the region bounded by y=|x-1| and y=1 in sq. units is

The area of the region bounded by y=|x-1| and y=1 in sq. units is

maths-General
maths-
The area of the elliptic quadratic with the semi major axis and semi minor axis as 6 and 4 respectively

The area of the elliptic quadratic with the semi major axis and semi minor axis as 6 and 4 respectively

maths-General
maths-
The area of circle circumscribing ΔABC is
The area of circle circumscribing ΔABC is
maths-General
maths-
Statement-I : The statement that circumradius and inradius of a triangle are 12 and 8 respectively can not be correct. Statement-II : Circumradius 2 (inradius)
Statement-I : The statement that circumradius and inradius of a triangle are 12 and 8 respectively can not be correct. Statement-II : Circumradius 2 (inradius)
maths-General
maths-
The complete solution set of the equation  is
is
The complete solution set of the equation  is
is
maths-General
Maths-
The solution(s) of the equation cos2x sin6x = cos3x sin5x in the interval [0, ] is/are –
] is/are –
The solution(s) of the equation cos2x sin6x = cos3x sin5x in the interval [0, ] is/are –
] is/are –
Maths-General
maths-
The equation  has
has
The equation  has
has
maths-General
maths-
 if
if
 if
if
maths-General