Physics-
General
Easy
Question
An object of mass 
is tied to a string of length 
and a variable horizontal force is applied on it which starts at zero and gradually increases until the string makes an angel 
with the vertical. Work done by the force 
is
The correct answer is:
or 
(Since, change in kinetic energy is zero)
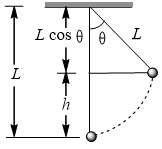
Here, 
work done by tension = 0
work done by fore of gravity
Related Questions to study
physics-
A block of mass 
kg sliding on a smooth horizontal surface with a velocity 
meets the spring of spring constant 
fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as is returns to the original position respectively are
A block of mass kg sliding on a smooth horizontal surface with a velocity meets the spring of spring constant fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as is returns to the original position respectively are
physics-General
physics-
The relationship between the force F and position 
of a body is as shown in figure. The work done in displacing the body from 
to 
m will be
The relationship between the force F and position of a body is as shown in figure. The work done in displacing the body from to m will be
physics-General
physics-
Three objects 
and 
are kept in a straight line on a frictionless horizontal surface. These have masses 
and respectively. The object 
moves towards 
with a speed 
and makes an elastic collision with it. Thereafter, makes completely inelastic collision with . All motions occur on the same straight line. Find the final speed (in 
) of the object
Three objects and are kept in a straight line on a frictionless horizontal surface. These have masses and respectively. The object moves towards with a speed and makes an elastic collision with it. Thereafter, makes completely inelastic collision with . All motions occur on the same straight line. Find the final speed (in ) of the object
physics-General
physics-
The relation between the displacement 
of an object produced by the application of the variable force is represented by a graph shown in the figure. If the object undergoes a displacement from 
to 
the work done will be approximately equal to
The relation between the displacement of an object produced by the application of the variable force is represented by a graph shown in the figure. If the object undergoes a displacement from to the work done will be approximately equal to
physics-General
physics-
In the given curved road, if particle is released from then
In the given curved road, if particle is released from then
physics-General
physics-
A body of mass 
slides down a curved track which is quadrant of a circle of radius 
. All the surfaces are frictionless. If the body starts from rest, its speed at the bottom of the track is
A body of mass slides down a curved track which is quadrant of a circle of radius . All the surfaces are frictionless. If the body starts from rest, its speed at the bottom of the track is
physics-General
physics-
A 10 kg brick moves along an -axis. Its acceleration as a function of its position is shown in figure. What is the net work performed on the brick by the force causing the acceleration as the brick moves from 
to 
m?
A 10 kg brick moves along an -axis. Its acceleration as a function of its position is shown in figure. What is the net work performed on the brick by the force causing the acceleration as the brick moves from to m?
physics-General
physics-
Force on a particle moving in a straight line varies with distance 
as shown in the figure. The work done on the particle during its displacement of 
Force on a particle moving in a straight line varies with distance as shown in the figure. The work done on the particle during its displacement of
physics-General
physics-
The potential energy of a system is represented in the first figure. The force acting on the system will be represented by
The potential energy of a system is represented in the first figure. The force acting on the system will be represented by
physics-General
physics-
The work done by force acting on a body is as shown in the graph. The total work done in covering an initial distance of 20 m is
The work done by force acting on a body is as shown in the graph. The total work done in covering an initial distance of 20 m is
physics-General
physics-
Two rectangular blocks 
and 
of masses 2kg and 3 kg respectively are connected by spring of spring constant 10.8 
and are placed on a frictionless horizontal surface. The block was given an initial velocity of 0.15 
in the direction shown in the figure. The maximum compression of the spring during the motion is
Two rectangular blocks and of masses 2kg and 3 kg respectively are connected by spring of spring constant 10.8 and are placed on a frictionless horizontal surface. The block was given an initial velocity of 0.15 in the direction shown in the figure. The maximum compression of the spring during the motion is
physics-General
physics-
Six identical balls are linked in a straight groove made on a horizontal frictionless surface as shown. Two similar balls each moving with a velocity 
collide elastically with the row of 6 balls from left. What will happen
Six identical balls are linked in a straight groove made on a horizontal frictionless surface as shown. Two similar balls each moving with a velocity collide elastically with the row of 6 balls from left. What will happen
physics-General
physics-
A force acting on an object varies with distance as shown here. The force is in 
and in 
. The work done by the force in moving the object from to 
is
A force acting on an object varies with distance as shown here. The force is in and in . The work done by the force in moving the object from to is
physics-General
physics-
What is the velocity of the bob of a simple pendulum at its mean position, if it is able to rise to vertical height of 
(Take 
)
What is the velocity of the bob of a simple pendulum at its mean position, if it is able to rise to vertical height of (Take )
physics-General
physics-
The block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant k and compresses it by length L. The maximum momentum of the block after collides is
The block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant k and compresses it by length L. The maximum momentum of the block after collides is
physics-General
