Physics
General
Easy
Question
The ratio of pathlength and the respective time interval is
- Mean velocity
- Mean speed
- instantaneous velocity
- instantaneous speed
The correct answer is: Mean speed
Related Questions to study
physics
A particle is thrown in upward direction with initial velocity of 60 m/s. Find average speed and average velocity after 10 seconds. [g =10 MS2]
A particle is thrown in upward direction with initial velocity of 60 m/s. Find average speed and average velocity after 10 seconds. [g =10 MS2]
physicsGeneral
physics-
The work done in deforming body is given by
The work done in deforming body is given by
physics-General
physics-
A wire of length 
and radius 
is stretched between 
and 
without the application of any tension. If 
is the Young’s modulus of the wire and it is stretched like 
, then the tension in the wire will be
A wire of length and radius is stretched between and without the application of any tension. If is the Young’s modulus of the wire and it is stretched like , then the tension in the wire will be
physics-General
physics-
A cube of aluminium of sides 0.1 m is subjected to a sharing force of 100 N. The top face of the cube is displaced through 0.02 cm with respect to the bottom face. The shearing strain would be
A cube of aluminium of sides 0.1 m is subjected to a sharing force of 100 N. The top face of the cube is displaced through 0.02 cm with respect to the bottom face. The shearing strain would be
physics-General
physics-
A uniform slender rod of length L, cross-sectional area A and Young’s modulus Y is acted upon by the forces shown in the figure. The elongation of the rod is
A uniform slender rod of length L, cross-sectional area A and Young’s modulus Y is acted upon by the forces shown in the figure. The elongation of the rod is
physics-General
physics-
The graph shows the behaviour of a length of wire in the region for which the substance obeys Hooke’s law. 
and 
represent
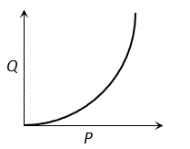
The graph shows the behaviour of a length of wire in the region for which the substance obeys Hooke’s law. and represent
physics-General
physics-
If the shear modulus of a wire material is 5.9
then the potential energy of a wire of 
in diameter and 5 cm long twisted through an angle of 10’ , is
If the shear modulus of a wire material is 5.9 then the potential energy of a wire of in diameter and 5 cm long twisted through an angle of 10’ , is
physics-General
physics-
The Young’s modulus of the material of a wire is equal to the
The Young’s modulus of the material of a wire is equal to the
physics-General
Maths-
Maths-General
physics-
Two short bar magnets of equal dipole moment M are fastened perpendicularly at their centers, figure. The magnitude of resultant of two magnetic field at a distance 
from the center on the bisector of the right angle is
Two short bar magnets of equal dipole moment M are fastened perpendicularly at their centers, figure. The magnitude of resultant of two magnetic field at a distance from the center on the bisector of the right angle is
physics-General
physics-
Two magnets of equal mass are joined at 90
each other as shown in figure. Magnet 
has a magnetic moment 
times that of 
. The arrangement is pivoted so that it is free to rotate in horizontal plane. When in equilibrium, what angle should make with magnetic meridian?
Two magnets of equal mass are joined at 90 each other as shown in figure. Magnet has a magnetic moment times that of . The arrangement is pivoted so that it is free to rotate in horizontal plane. When in equilibrium, what angle should make with magnetic meridian?
physics-General
physics-
The pressure applied from all directions on a cube is . How much its temperature should be raised to maintain the original volume? The volume elasticity of the cube is 
and the coefficient of volume expansion is 
The pressure applied from all directions on a cube is . How much its temperature should be raised to maintain the original volume? The volume elasticity of the cube is and the coefficient of volume expansion is
physics-General
physics-
A wire 
has length 1 m and cross-sectional area 1 
The work required to increase the length by 2 mm is
A wire has length 1 m and cross-sectional area 1 The work required to increase the length by 2 mm is
physics-General
physics-
The diagram shows a force-extension graph for a rubber band. Consider the following statements
I. It will be easier to compress this rubber than expand it
II. Rubber does not return to its original length after it is stretched
III. The rubber band will get heated if it is stretched and released
Which of these can be deduced from the graph
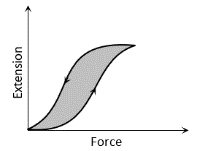
The diagram shows a force-extension graph for a rubber band. Consider the following statements
I. It will be easier to compress this rubber than expand it
II. Rubber does not return to its original length after it is stretched
III. The rubber band will get heated if it is stretched and released
Which of these can be deduced from the graph
physics-General
physics-
A wire of length Land radius 
rigidly fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is 
If another wire of same material but of length 2L and radius 
is stretched with a force 2F, the increase in its length will be
A wire of length Land radius rigidly fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is If another wire of same material but of length 2L and radius is stretched with a force 2F, the increase in its length will be
physics-General
