Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

The pressure applied from all directions on a cube is $P$ . How much its temperature should be raised to maintain the original volume? The volume elasticity of the cube is $beta$ and the coefficient of volume expansion is $alpha$

$\frac{P}{α β}$
$\frac{P α}{β}$
$\frac{P β}{α}$
$\frac{α β}{P}$

The correct answer is: $fraction numerator P over denominator alpha beta end fraction$

If coefficient of volume expansion is $alpha$ and rise in temperature is $increment theta$ then $increment V equals V alpha increment theta rightwards double arrow fraction numerator increment V over denominator V end fraction equals alpha increment theta$
Volume elasticity $beta equals fraction numerator P over denominator increment V divided by V end fraction equals fraction numerator P over denominator alpha increment theta end fraction rightwards double arrow increment theta equals fraction numerator P over denominator alpha beta end fraction$

Related Questions to study

A wire $left parenthesis Y equals 2 cross times 10 to the power of 11 end exponent N m to the power of negative 2 end exponent right parenthesis$ has length 1 m and cross-sectional area 1 $m m to the power of negative 2 end exponent.$ The work required to increase the length by 2 mm is

A wire $left parenthesis Y equals 2 cross times 10 to the power of 11 end exponent N m to the power of negative 2 end exponent right parenthesis$ has length 1 m and cross-sectional area 1 $m m to the power of negative 2 end exponent.$ The work required to increase the length by 2 mm is

physics-General

The diagram shows a force-extension graph for a rubber band. Consider the following statements
I. It will be easier to compress this rubber than expand it
II. Rubber does not return to its original length after it is stretched
III. The rubber band will get heated if it is stretched and released
Which of these can be deduced from the graph

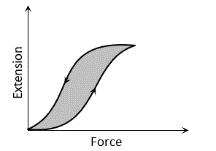
The diagram shows a force-extension graph for a rubber band. Consider the following statements
I. It will be easier to compress this rubber than expand it
II. Rubber does not return to its original length after it is stretched
III. The rubber band will get heated if it is stretched and released
Which of these can be deduced from the graph

physics-General

A wire of length Land radius $a$ rigidly fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is $l.$ If another wire of same material but of length 2L and radius $2 a$ is stretched with a force 2F, the increase in its length will be

A wire of length Land radius $a$ rigidly fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is $l.$ If another wire of same material but of length 2L and radius $2 a$ is stretched with a force 2F, the increase in its length will be

physics-General

parallel

The variation of intensity of magnetization $left parenthesis I right parenthesis$ with respect to the magnetizing field (H) in a diamagnetic substance is described by the graph in figure.

The variation of intensity of magnetization $left parenthesis I right parenthesis$ with respect to the magnetizing field (H) in a diamagnetic substance is described by the graph in figure.

physics-General

The number of one one onto functions that can be defined from A={a,b,c,d} into B={1,2,3,4} is

The number of one one onto functions that can be defined from A={a,b,c,d} into B={1,2,3,4} is

The number of ways one can arrange words with the letters of the word ’ so that ↑MADHURI↑ always vowels occupy the beginning, middle and end places is

The number of ways one can arrange words with the letters of the word ’ so that ↑MADHURI↑ always vowels occupy the beginning, middle and end places is

parallel

If $f colon R not stretchy rightwards arrow left parenthesis 0 comma 1 right square bracket$ defined by $f left parenthesis x right parenthesis equals fraction numerator 1 over denominator x squared plus 1 end fraction comma text then end text f text is end text$

If $f colon R not stretchy rightwards arrow left parenthesis 0 comma 1 right square bracket$ defined by $f left parenthesis x right parenthesis equals fraction numerator 1 over denominator x squared plus 1 end fraction comma text then end text f text is end text$

An ant goes from P to Q on a circular path in 20 second Radius OP=10 m . What is the average speed and average velocity of it ?

An ant goes from P to Q on a circular path in 20 second Radius OP=10 m . What is the average speed and average velocity of it ?

Which of the following functions is not injective?

Which of the following functions is not injective?

parallel

The graph of position $not stretchy rightwards arrow$ time shown in the figure for a particle is not possible because ....

The graph of position $not stretchy rightwards arrow$ time shown in the figure for a particle is not possible because ....

Curie-Weiss law is obeyed by iron

Curie-Weiss law is obeyed by iron

physics-General

If the $B minus H$ curves of two samples of P and Q of iron are as shown below, then which one of the following statements is correct?

If the $B minus H$ curves of two samples of P and Q of iron are as shown below, then which one of the following statements is correct?

physics-General

parallel

Among the following properties describing diamagnetism identify the property that is wrongly stated

Among the following properties describing diamagnetism identify the property that is wrongly stated

physics-General

Permanent magnet has properties retentivity and coercivity respectively

Permanent magnet has properties retentivity and coercivity respectively

physics-General

The magnetic susceptibility of a paramagnetic substance at $negative 73 degree$ C is 0.0060, then its value at $negative 173 degree$ C will be

The magnetic susceptibility of a paramagnetic substance at $negative 73 degree$ C is 0.0060, then its value at $negative 173 degree$ C will be

physics-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.