Maths-
General
Easy
Question
The distribution of a random variable X is given below
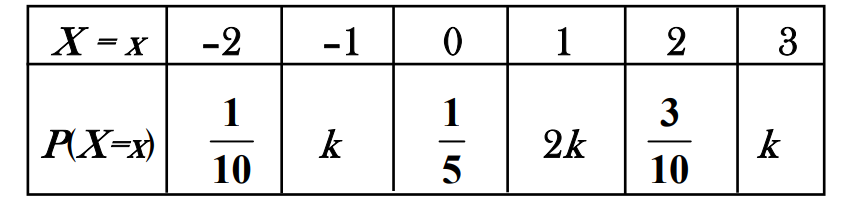
The value of k is

We know that, Sum of all the probabilities in an event = 1. Use this to find out the answer.
The correct answer is: 
We know that,
Sum of all the probabilities in an event = 1
P(x= -2) + P(x= -1) + P(x= 0) + P(x= 1) + P(x= 2) + P(x= 3) = 1

Related Questions to study
maths-
The number of different triangles formed by joining the points A, B, C, D, E, F and G as shown in the figure given below is

The number of different triangles formed by joining the points A, B, C, D, E, F and G as shown in the figure given below is

maths-General
maths-
The number of ways that the letters of the word ”PERSON” can be placed in the squares of the adjoining figure so that no row remains empty

The number of ways that the letters of the word ”PERSON” can be placed in the squares of the adjoining figure so that no row remains empty



maths-General
maths-
The value of  is
is
The value of  is
is
maths-General
maths-
The determinant  is equal to zero if
is equal to zero if  are in
are in
The determinant  is equal to zero if
is equal to zero if  are in
are in
maths-General
Maths-
If  satisfy
satisfy  then
then 
If  satisfy
satisfy  then
then 
Maths-General
chemistry-
End product of the following sequence of reaction is :

End product of the following sequence of reaction is :

chemistry-General
chemistry-
Arrange in the increasing order of boiling points:
i) 
ii) 
iii) 
iv) 
Arrange in the increasing order of boiling points:
i) 
ii) 
iii) 
iv) 
chemistry-General
maths-
Number of rectangles in fig. shown which are not squares is

Number of rectangles in fig. shown which are not squares is

maths-General
maths-
Digit at unit place of sum (1!)2 +(2!)2 +(3!)2 ……… +(2008!)2 is
Digit at unit place of sum (1!)2 +(2!)2 +(3!)2 ……… +(2008!)2 is
maths-General
maths-
A person writes letters to 6 friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that at least 4 of them are in wrong envelopes ?
A person writes letters to 6 friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that at least 4 of them are in wrong envelopes ?
maths-General
maths-
The total numbers of integral solutions for (x,y,z) such that xyz = 24 is
The total numbers of integral solutions for (x,y,z) such that xyz = 24 is
maths-General
maths-
Number of ways in which 5 different toys can be distributed among 5 children if exactly one child do not get any toy
Number of ways in which 5 different toys can be distributed among 5 children if exactly one child do not get any toy
maths-General
maths-
A seven digit number is in form of abcdefg (g, f, e, etc. are digits at units, tens, hundred place etc.) where a < b < c < d > e > f > g. The number of such numbers are
A seven digit number is in form of abcdefg (g, f, e, etc. are digits at units, tens, hundred place etc.) where a < b < c < d > e > f > g. The number of such numbers are
maths-General
maths-
Number of ways in which 25 identical balls can be distributed among Ram, Shyam, Sunder and Ghanshyam such that atleast 1, 2, 3, and 4 balls are given to Ram, Shyam, Sunder and Ghanshyam respectively, is-
Number of ways in which 25 identical balls can be distributed among Ram, Shyam, Sunder and Ghanshyam such that atleast 1, 2, 3, and 4 balls are given to Ram, Shyam, Sunder and Ghanshyam respectively, is-
maths-General
maths-
One hundred identical marbles are to be distributed to three children so that each gets atlest 20 and no two get equal number. The number of ways of doing this is -
One hundred identical marbles are to be distributed to three children so that each gets atlest 20 and no two get equal number. The number of ways of doing this is -
maths-General



