Question
The number of points in the Cartesian plane with integral co-ordinates satisfying the inequalities |x|  k, |y|
k, |y|  k, |x – y|
k, |x – y|  k ; is-
k ; is-
- (k + 1)3 – k3
- (k + 2)3 – (k +1)3
- (k2 + 1)
- None of these
The correct answer is: (k + 1)3 – k3
|x|  k
k  –k
–k  x
x  k ….(1)
k ….(1)
& |y|  k
k  –k
–k  y
y  k ….(2)
k ….(2)
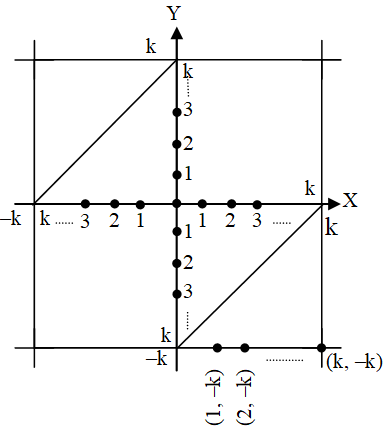
& |x – y|  k
k  |y – x|
|y – x|  k
k  –k
–k  y – x
y – x  k
k  x – k
x – k  y
y  x + k ….(3)
x + k ….(3)
 Number of points having integral coordinates
Number of points having integral coordinates
= (2k + 1)2 – 2
= (3k2 + 3k + 1).
Related Questions to study
The angle between the lines  and
and  is
is
Here we used the concept of cartesian lines and some trigonometric terms to solve. With the help of slope we identified the angle between them. Hence, these lines are perpendicular so the angle between them is 90 degrees.
The angle between the lines  and
and  is
is
Here we used the concept of cartesian lines and some trigonometric terms to solve. With the help of slope we identified the angle between them. Hence, these lines are perpendicular so the angle between them is 90 degrees.
The polar equation of the straight line passing through  and perpendicular to the initial line is
and perpendicular to the initial line is
The polar equation of the straight line passing through  and perpendicular to the initial line is
and perpendicular to the initial line is
The polar equation of the straight line passing through  and parallel to the initial line is
and parallel to the initial line is
The polar equation of the straight line passing through  and parallel to the initial line is
and parallel to the initial line is
The equation of the line passing through pole and  is
is
The equation of the line passing through pole and  is
is
The polar equation of  is
is
Here we used the concept of polar coordinate system and also the trigonometric ratios to find the solution. So the equation is .
The polar equation of  is
is
Here we used the concept of polar coordinate system and also the trigonometric ratios to find the solution. So the equation is .
The cartesian equation of  is
is
Here we used the concept of the polar coordinate system and also the trigonometric ratios to find the solution. So the equation is .
The cartesian equation of  is
is
Here we used the concept of the polar coordinate system and also the trigonometric ratios to find the solution. So the equation is .
Two tuning forks  and
and  are vibrated together. The number of beats produced are represented by the straight line
are vibrated together. The number of beats produced are represented by the straight line  in the following graph. After loading
in the following graph. After loading  with wax again these are vibrated together and the beats produced are represented by the line
with wax again these are vibrated together and the beats produced are represented by the line  If the frequency of
If the frequency of  is
is  the frequency of
the frequency of  will be
will be

Two tuning forks  and
and  are vibrated together. The number of beats produced are represented by the straight line
are vibrated together. The number of beats produced are represented by the straight line  in the following graph. After loading
in the following graph. After loading  with wax again these are vibrated together and the beats produced are represented by the line
with wax again these are vibrated together and the beats produced are represented by the line  If the frequency of
If the frequency of  is
is  the frequency of
the frequency of  will be
will be

If a hyperbola passing through the origin has  and
and  as its asymptotes, then the equation of its tranvsverse and conjugate axes are
as its asymptotes, then the equation of its tranvsverse and conjugate axes are
Here we used the concept of polar coordinate system and also the trigonometric ratios to find the solution.
If a hyperbola passing through the origin has  and
and  as its asymptotes, then the equation of its tranvsverse and conjugate axes are
as its asymptotes, then the equation of its tranvsverse and conjugate axes are
Here we used the concept of polar coordinate system and also the trigonometric ratios to find the solution.



