Key Concepts
- Use models and properties to divide with 2-digit divisor
- Use partial quotients to divide
Introduction
- Find the quotients using area models
- Use distributive property to find the quotients
- Solve different questions on the division of whole numbers
- Understand the estimation to solve divisions
- Use partial quotients to divide
- Use diagrams to divide partial quotients.
Use models and properties to divide with 2-digit divisors
What is an area model?
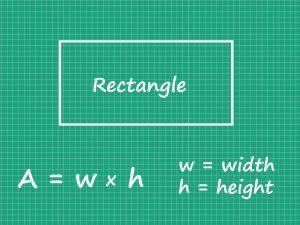
An area model is a rectangular diagram or model used to solve multiplication and division problems.
What is a rectangular model?
The area model is a rectangular figure used to solve multiplication and division problems, in which the factors or quotient and divisor determine the rectangle’s length and width.
How to solve multiplication and division using area models?
Generally, multiplication and division problems can be solved using a rectangle area model.
Divide a large rectangle into several smaller boxes, using number bonds, to make the calculation easier. Then, add to get the area of the whole, which is the product or the quotient.
The following steps explain’s the multiplication and division of two 2-digit numbers using an area model:
- Write the multiplicands in expanded form as tens and ones.
For example, 33 as 30 and 3, and 25 as 20 and 5. - Draw a 2 × 2 grid box with 2 rows and 2 columns.
- Write the terms of one of the multiplicands on the top of the grid (box). One on the top of each cell.
- On the left of the grid, write the terms of the other multiplicand. One on the side of each cell.
- Write the product of the number of tens in the first cell. Then write the product of the tens and ones in the second and third cell. Write the product of the ones in the fourth cell.

- Add all the partial products to get the product.
For instance, the following area model used to multiply 17 and 25.

Now we use the area model for the division. Here, we divide 625 by 5.

Example 1:
Solve 87 ÷ 5 by using an area model. Use long division and the distributive property to divide.
Solution:

Use partial quotients to divide
How can you use partial quotients to solve division problem?
For instance, use partial quotients to divide 536 ÷ 4.
Solution:
Step 1: Write the given problem in long division method.

Step 2: Re – write the divisor and dividend into partial quotients.

Step 3: Now, calculate the difference of the dividend and the product of the divisor.

Step 4: Partial quotient must be written on the top.

Step 5: Until we get the difference as zero, continue to find the partial quotients.

Step 6: Add all the partial quotients.

Example 1:
Divide using partial quotients.
Solution:

Exercise
- Use the diagram to find 375 ÷ 25.
- A rectangular doormat is 21 inches long and has an area of 714 square inches. Find the width of the doormat.
- Divide using partial quotient.
- How can you use partial quotients to divide 225 ÷ 13?
- Draw a picture to divide 168 ÷ 24.
- Divide 848 ÷ 4 using an area model.
- Draw a diagram to divide 8,304 ÷ 24.
- Use partial quotients, divide .
- Use partial quotients, divide .
- Divide using diagram, 240 ÷ 20.
What We Have Learned
- Find the quotients using area models
- Use distributive property to find the quotients
- Solve different questions on division of whole numbers
- Understand the estimation to solve divisions
- Use partial quotients to divide
- Use diagrams to divide partial quotients.
Summary
Key Points:
- Long division: The process to solve a division problem.
- Quotient: If a number is divided by another number, the resulting answer is known as quotient.
Ex: 27 ÷ 3 = 9, the number 9 is the quotient. - Remainder: If a whole number is divided by another whole number, then the left-over number is called the remainder.
Ex: 36 ÷ 7 = 5 here the remainder is 1. - Distributive Property: The property of multiplication that is used to create easy problems.
Ex: 7 × 5 = (6 × 5) + (1×5). - Area Model: An area model is a rectangular diagram or model used for solve multiplication and division problems.
Related topics
Addition and Multiplication Using Counters & Bar-Diagrams
Introduction: We can find the solution to the word problem by solving it. Here, in this topic, we can use 3 methods to find the solution. 1. Add using counters 2. Use factors to get the product 3. Write equations to find the unknown. Addition Equation: 8+8+8 =? Multiplication equation: 3×8=? Example 1: Andrew has […]
Read More >>Dilation: Definitions, Characteristics, and Similarities
Understanding Dilation A dilation is a transformation that produces an image that is of the same shape and different sizes. Dilation that creates a larger image is called enlargement. Describing Dilation Dilation of Scale Factor 2 The following figure undergoes a dilation with a scale factor of 2 giving an image A’ (2, 4), B’ […]
Read More >>How to Write and Interpret Numerical Expressions?
Write numerical expressions What is the Meaning of Numerical Expression? A numerical expression is a combination of numbers and integers using basic operations such as addition, subtraction, multiplication, or division. The word PEMDAS stands for: P → Parentheses E → Exponents M → Multiplication D → Division A → Addition S → Subtraction Some examples […]
Read More >>System of Linear Inequalities and Equations
Introduction: Systems of Linear Inequalities: A system of linear inequalities is a set of two or more linear inequalities in the same variables. The following example illustrates this, y < x + 2…………..Inequality 1 y ≥ 2x − 1…………Inequality 2 Solution of a System of Linear Inequalities: A solution of a system of linear inequalities […]
Read More >>Other topics






Comments: