Key Concepts
- Use arrays for partial products
- Use of area for partial products
Introduction:
- In this chapter, we will learn about the introduction of array.
- About partial products
- Use arrays in partial products
- Area of rectangle
- Area for partial products
Use arrays for partial products
Partial products:
A product obtained by multiplying a multiplicand by one digit of a multiplier having more than one digit.
Example: 1
Find the product for 3 × 14.
In the below image indicate using arrays for partial products.

From the above image
The numbers 30 and 12 are called partial products.
42 is the product.
Another way:
14
× 3
______
12 3 × 4 ones
+ 30 3 × 1 tens
_______
42
______
The product 42 is close to the estimate 40. The answer is reasonable.
We can use place value to break factors and distributive property to find partial products.
Example: 2
Multiply 3 × 46

Break 46 into two parts: 40 and 6.
Then, multiply those two parts separately by 3:
3 × 40 is 120, and 3 × 6 is 18.
Then, add these two partial results: 120 + 18 = 138
138 is close to 130
Note: We can use place value to break factors and the distributive property to find the partial products.
Let us see another example:
Find 2 × 124
Estimate:
2 × 124 is about 2 × 100 = 200


Open array:

Here, we can use the distributive property
3 × 14 = (3 × 10) +(3 × 4)
3.4 Use of area for partial products
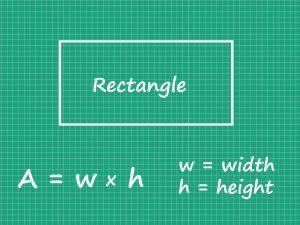
Area is the region bounded by the shape of an object. The space covered by the figure or any geometric shapes is the area of the shape.
Area of rectangle = Length × Breadth
A = lb
Example1:
A park is in the shape of a rectangle. It is 6 feet wide and 24 feet long. What is the area of the park?
6 × 24 is a numerical expression

We can use rectangular area model to show multiplication.
The product of 6 × 24 is the area of the rectangle.
Estimate 6 × 24 is about 6 × 20 = 120

120 + 24 = 144
The distributive property says that the sum of numbers is same as multiplying each part of the sum by that number and adding the partial products.
6 × 24 = (6 × 20) + (6 × 4)
Another way:
2 4
× 6
_________
2 4 6 × 4 ones
+ 1 2 0 6 × 2 tens
_________
1 4 4
The area of the park is 144 square feet.
The product, 144 is close to the estimate of 120. The answer is reasonable.
Example 2:
Find the area of 8 × 24

The picture illustrates the area of a rectangle with sides 8 and 24. It is also divided into two rectangles.
The area of the whole rectangle is 8 × 24 square units.
We can find that by calculating the areas of the two rectangles and adding.
The area of the first rectangle is 8 × 20 = 160 square units.
The area of the second rectangle is 8 × 4 = 32 square units.
So, the area of the whole rectangle is the sum 160 + 32 = 192 square units.
Another way
2 4
× 8
_______________
32 8 × 4
+ 160 8 × 20
_______________
1 9 2
Exercise:
- Solve the following problems using partial products:
a) 87 × 4 b) 78 × 6 c) 32 × 5 - Solve using arrays.
148 × 3 b) 409 × 2 c) 306 × 4 - Explain how can you found the product of 3 and 57.
- Explore different ways to understand multiplying a three-digit number by a one-digit number.
What is the product of 3 and 254? - What will be the cost of gardening a 1 meter broad boundary around a rectangular plot having a perimeter of 340 meters at the rate of Rs. 8 per square meter?
- Draw a model to represent the product.
Then record the product.
a) 3 × 42 b) 8 × 34 c) 2 × 26 - What product does the model below represent?

8. A rectangular room has a length of 16 feet and a width of 8 feet. How much carpet is required to cover the entire room?
9.The length and width of a rectangular farm are 80 yards and 6 yards. Find the area of the farm.
10.Find the total distance around the rectangular field, if the length of the field is 50 meters and width is 8 meters. Also, find the area of the field.
What have we learned:
- Introduction of array.
- Introduction of partial products
- Use arrays in partial products
- Area of rectangle
- Area for partial products
Concept map:


Related topics
Addition and Multiplication Using Counters & Bar-Diagrams
Introduction: We can find the solution to the word problem by solving it. Here, in this topic, we can use 3 methods to find the solution. 1. Add using counters 2. Use factors to get the product 3. Write equations to find the unknown. Addition Equation: 8+8+8 =? Multiplication equation: 3×8=? Example 1: Andrew has […]
Read More >>Dilation: Definitions, Characteristics, and Similarities
Understanding Dilation A dilation is a transformation that produces an image that is of the same shape and different sizes. Dilation that creates a larger image is called enlargement. Describing Dilation Dilation of Scale Factor 2 The following figure undergoes a dilation with a scale factor of 2 giving an image A’ (2, 4), B’ […]
Read More >>How to Write and Interpret Numerical Expressions?
Write numerical expressions What is the Meaning of Numerical Expression? A numerical expression is a combination of numbers and integers using basic operations such as addition, subtraction, multiplication, or division. The word PEMDAS stands for: P → Parentheses E → Exponents M → Multiplication D → Division A → Addition S → Subtraction Some examples […]
Read More >>System of Linear Inequalities and Equations
Introduction: Systems of Linear Inequalities: A system of linear inequalities is a set of two or more linear inequalities in the same variables. The following example illustrates this, y < x + 2…………..Inequality 1 y ≥ 2x − 1…………Inequality 2 Solution of a System of Linear Inequalities: A solution of a system of linear inequalities […]
Read More >>Other topics






Comments: