Key Concepts
- Multiplying with a One-digit Number
- Multiplication as Repeated Addition
- Multiplication as a Rectangular Array and Area of a Rectangle
- Multiply Using the Place Value of Each Digit
- Multiplying with a Two-digit Number
- Estimate the Products
- Modeling Division with Regrouping in Hundreds, Tens, and Ones
- Dividing by a One-digit Number to Find Quotient and Remainder with Estimating
- Real-world problems: Multiplication and Division.
3.1: Multiplying with a One-digit Number
3.1.1: Representing Multiplication as Repeated Addition.
Definition of multiplication: It is known as repeated addition. It is denoted by ‘×’ or ‘.’, and the parts of multiplication include ‘multiplicand’, ‘multiplier’ and ‘product’, which is the result.

Rules: Multiplication of integer rules:

Example: Find as repeated addition.

Sol.: Here, there are three groups, and each group has four dogs.
3 × 4 = 12

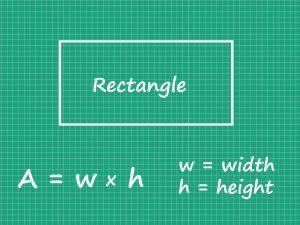
3.2.1: Representing Multiplication as Rectangular Array and the Area of a
Rectangle.
Array: An array is formed by arranging a set of objects into rows and columns. Each column must contain the same number of objects as the other columns, and each row must have the same numbers as the other rows.
Example: Find 215 × 3. Draw an array to find the answer.
| Hundreds | Tens | Ones |
| 0 0 0 0 0 0 | 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
| 2 H × 3 | 1 T × 3 | 5 O × 3 |
Sol.: 215 × 3
3 × 215 = 5 × 3 + 10 × 3 + 200 × 3
= 15 + 30 + 600
= 645
Example: Find 215 × 3 by using an area of a rectangle.
Sol.:

Area of whole rectangle
= l × w
= 215 × 3
Area of whole rectangle = 645
= Area of rectangle C + area of rectangle B + area of rectangle A
215 × 3 = 5 × 3 + 10 × 3 + 200 × 3
645 = 15 + 30 + 600
645 = 645
3.1.3: Multiplication Using the Place Value of Each Digit.
Place value: Place value is the value of each digit in a number.
Place Value Chart:

Example: Multiply 3417 × 5 using the place value of each digit.
Sol.:

3.2: Multiplying by a Two-digit Number
3.2.1: Multiplying by Two-digit Numbers.
Example: Find the product of 50 × 9.
Sol.: = 50 × 9
Example: Find the product of 24 × 200.
Sol.: 24 × 200 = 24 × 100 × 2
= 2400 × 2
= 4800
Example: Round 3839 and 7220 to nearest hundreds.
3.2.2: Estimate the Products.
Rounded: 26 is 30 when rounded to nearest tens.
Sol.:

Estimate: A number close to the exact number is an estimate.
Example: Estimate the product of 272 and 21.
Sol.:

Example: Estimate the product of 32 × 215.
Sol.: 32 is closer to 30.
215 is closer to 220.
So, 30 × 220 = 6600
3.3: Modeling Division with Regrouping
3.3.1: Model Division with Regrouping in Hundreds, Tens and Ones.
Regrouping: To regroup means to rearrange groups in place value to carry out an operation.
Example: Find 468 ÷ 3.
Sol.: Follow the steps to divide.
Step–1: Begin with the hundreds digit.
4 hundred ÷ 3 = 1 hundred with remainder 1 hundred

Regroup the hundreds
1 hundred = 10 tens
Add the tens.
10 tens + 6 tens = 16 tens

Step–2: Divide the tens by 3.
16 tens ÷ 3 = 5 tens

Regroup the tens.
1 tens = 10 ones
Add the ones.
10 ones + 8 ones = 18 ones

Step–3: Divide the ones by 3.
18 ones ÷ 3 = 6 ones

So, 465 ÷ 3 = 156
3.4: Dividing by a One-Digit Number
Definition: Division is the inverse of multiplication or repeated subtraction. It is denoted by ‘÷’.

Rules:

Example: Find 8 ÷ 4.
3.4.1: Finding the Quotients and the Remainder.
Quotient: A quotient is an answer to a division problem.
Example: Fine the quotient of 4258 ÷ 2.
Sol.:

Remainder: A remainder is the number left over when a number cannot be divided evenly or entirely.
Example: Find the remainder of 5084 ÷ 4
Sol.:

3.4.2: Estimation of the Quotients.
To estimate the quotient, we first round off the divisor and the dividend to the nearest tens, hundreds or thousands and then divide the rounded numbers.
Example: Divide 242 ÷ 22.
Sol.: Round to the nearest ten.

Estimated Quotient = 12
3.5. Real -world problems
Word problem: A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved through a mathematical calculation.
3.5.1: Solving Word Problems on Multiplication and Division.
Example: The cost of a chair is $450. Find the cost of such 120 chairs.
Sol.: Cost of a chair = 450
Number of chairs = 120

Cost of 120 chairs = $54,000
Example: 12 candies are divided among 3 children. How many candies will each child get?
Sol.:

Example: The cost of 124 train tickets was $24,648. Find the cost of one ticket.
Sol.: Number of train tickets = 124
Cost of 124 train tickets = $24,048
Cost of 1 train ticket = 24,648 ÷ 124

The cost of one train ticket is $198.7.
3.5.2: Multi-Step Word Problems.
Multi-step word problems are a mix of addition, subtraction, multiplication, and division, all written using whole numbers.
Example:
A pair of jeans costs $89, a jeans jacket costs twice as much. What is the total cost of a jeans jacket and 5 pairs of jeans?
Sol.: Given pair of jeans costs = $89
5 pairs of jeans = 5 × 89
= $445
A jeans jacket cost twice of jeans = 89 + 89
= $178
Total = 445
178
$623
Exercise:
- Find 250 × 2 by using repeated addition.
- Find 420 × 5 by using repeated addition.
- Find 320 × 4. Draw an array to find the answer.
- Find 515 × 2 by using an array rectangle.
- Find 5432 × 2 by using place value.
- Find the product of 20 × 5.
- Find the product of 54 × 350.
- Estimate the product of 45 × 26.
- Find 254 ÷ 2.
- Find the quotient of 5423 ÷ 5.
- Find the remainder of 243 ÷ 3.
- Find the quotient and remainder of 2567 ÷ 4.
- Estimate the quotient of 543 ÷11.
- 20 people can fit in 4 rooms. How many people can fit in 70 rooms?
- Calvin makes quilts; he can make one quilt with 21 yards of material. How many yards of material would be required to make 15 quilts?
Concept Map:

What have we learned:
In this chapter, we learned:
- About examining the difference between multiplication and division.
- About multiplying a whole number of up to four digits by a one-digit whole number and multiplying two-digit numbers using strategies based on place value.
- Calculation by using rectangular arrays and area models.
- Division with regrouping hundreds, tens and ones.
- Estimating products and quotients.
- How to find quotient and remainder.
- To solve one step and multi-step word problems using different operations.
Related topics
Addition and Multiplication Using Counters & Bar-Diagrams
Introduction: We can find the solution to the word problem by solving it. Here, in this topic, we can use 3 methods to find the solution. 1. Add using counters 2. Use factors to get the product 3. Write equations to find the unknown. Addition Equation: 8+8+8 =? Multiplication equation: 3×8=? Example 1: Andrew has […]
Read More >>Dilation: Definitions, Characteristics, and Similarities
Understanding Dilation A dilation is a transformation that produces an image that is of the same shape and different sizes. Dilation that creates a larger image is called enlargement. Describing Dilation Dilation of Scale Factor 2 The following figure undergoes a dilation with a scale factor of 2 giving an image A’ (2, 4), B’ […]
Read More >>How to Write and Interpret Numerical Expressions?
Write numerical expressions What is the Meaning of Numerical Expression? A numerical expression is a combination of numbers and integers using basic operations such as addition, subtraction, multiplication, or division. The word PEMDAS stands for: P → Parentheses E → Exponents M → Multiplication D → Division A → Addition S → Subtraction Some examples […]
Read More >>System of Linear Inequalities and Equations
Introduction: Systems of Linear Inequalities: A system of linear inequalities is a set of two or more linear inequalities in the same variables. The following example illustrates this, y < x + 2…………..Inequality 1 y ≥ 2x − 1…………Inequality 2 Solution of a System of Linear Inequalities: A solution of a system of linear inequalities […]
Read More >>Other topics






Comments: